Complexidade de Algoritmos - Um Texto Introdutório

Introdução

O desenvolvimento de algoritmos é uma das principais tarefas dos programadores e cientistas da computação e um grande desafio também. Um problema, muitas vezes, poder ser resolvido por vários algoritmos diferentes. O desafio nesse caso é selecionar qual é o mais eficiente entre eles, ou seja, qual exigirá menos capacidade de processamento do computador e menos recursos do sistema.

Esta postagem busca dar uma visão geral do assunto sem apresentar aspectos teóricos da teoria da complexidade de de algoritmos.

Por mais que os computadores se tornem mais potentes com o passar dos anos, a demanda por algoritmos complexos também aumenta. Por exemplo:

• Algoritmos para resolver equações complicadas (equações diferenciais e sistemas de equações diferenciais, por exemplo);
• Algoritmos para realizar cálculos de precisão envolvendo astronomia e mecânica quântica;
• Algoritmos para simular fenômenos físicos, meteorológicos, financeiros, etc;
• Algoritmos para simular projetos de uma forma geral, antes que eles sejam desenvolvidos na prática;
• Algoritmos para processar um grande volume de dados;
• Entre outros.

No contexto das aplicações citadas, um algoritmo mais eficaz pode significar ganho de tempo para realizar outras tarefas, economia de recursos financeiros, prevenção antecipada de desastres naturais (modelagem climática); etc.

Também vale ressaltar que algoritmos mais eficientes são extremamente importantes para sistemas embarcados e dispositivos móveis (celulares, pagers, video games portáteis, etc), pois um algoritmo mais eficaz reduz o consumo de bateria (já que irá exigir menos capacidade de processamento).

Resumindo, da mesma forma que é necessária a criação de computadores mais potentes, também é necessária a criação de algoritmos mais eficientes.

O Conceito Básico de Complexidade de Algoritmos

Tal complexidade depende da quantidade de dados que o algoritmo recebe e dos dados em si (nos preocupemos apenas com a quantidade de dados a princípio). Quanto maior a quantidade de dados, maior a quantidade de operações ou passos que o algoritmo irá realizar para concluir sua tarefa. Consequentemente o tempo de execução desse algoritmo também aumentará.

Ao analisar algoritmos, pode-se representar a quantidade de operações realizadas em função da quantidade de dados (ou tamanho da entrada de dados). Ou seja, usa-se uma função matemática para definir a complexidade dos algoritmos.

Com isso, fica mais fácil analisar qual é o algoritmo mais eficiente, pois basta comparar as funções de suas complexidades e situações de uso do algoritmo.

A tabela a seguir foi retirada de um slide do Instituto de Matemática e Estatística da Universidade de São Paulo (IME/USP). Está disponível para consulta no link: Complexidade de Algoritmos

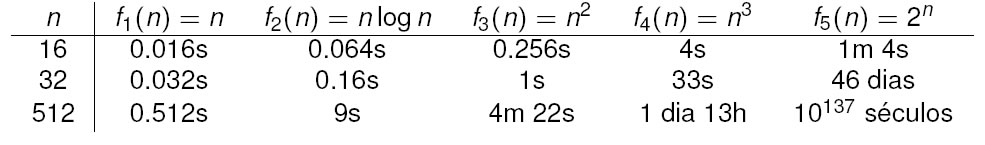
• n é equivalente ao tamanho da entrada de dados ou quantidade de dados;
• f1(n), f2(n), f3(n), f4(n) e f5(n) são funções que representam a complexidade de diferentes algoritmos, mostrando quanto tempo ou quantidade de operações que o algoritmo realiza em função da quantidade ou volume de dados de entrada;

Observação: o log da função f2(n) da tabela, é o logaritmo na base 2.

Em tais algoritmos, supõe-se que cada operação demora um milissegundo para ser executada. Na verdade, o tempo em si é bem relativo, pois depende do computador que executa o algoritmo

Observe que o algoritmo representado pela função f5(n) tem o pior tempo de execução de todos, pois é uma função exponencial. Neste caso, podemos dizer que o algoritmo roda em tempo exponencial.

Conclusão

Analisar a complexidade de algoritmos e estimar quanto tempo ele irá demorar para ser executado é uma tarefa muito importante, pois determina o quão eficiente um algoritmo pode ser e se o mesmo é viável ou não para um determinado sistema.

A escolha de um algoritmo mais eficiente em sistemas que lidam com operações ou cálculos complexos ou então que processam um grande volume de dados pode significar um ganho de tempo valioso, podendo ser usado para realização de outras tarefas.

A utilização de fórmulas matemáticas para expressar a complexidade de um algoritmo é uma das melhores formas de ilustrar e comparar quantas operações serão realizadas por ele de acordo com a quantidade de dados de entrada.

Por fim, é importante salientar que na análise da complexidade de um algoritmo não devemos nos limitar apenas em analisar fórmulas matemáticas. É essencial ver como o algoritmo irá funcionar na prática, em situações reais, e também analisar seu código. Muitas vezes, um algoritmo mais eficaz pode resultar em códigos extensos e complicados de entender. Cabe ao programador ter uma visão global do que está fazendo e decidir qual é a melhor opção.

Referências

• [1] CORMEN, Thomas H; et al. Algoritmos - Teoria e Prática. 3ª edição. São Paulo: Elsevier - Campus, 2012
• [2] SONG, Siang Wun. Complexidade de Algoritmos (MAC 5710 - Estruturas de Dados). IME/USP: 2008.

Observações

Revisado por Aurélio Araújo (Sistemas de Informações - FAP/CE), que também sugeriu a parte sobre sistemas embarcados e dispositivos móveis.