Estruturas de dados são conjuntos de dados organizados de forma estratégica, cujo intuito é realizar operações sobre esses dados de forma eficiente, dependendo, é claro, do tipo de aplicação considerada.

Operações típicas de uma estrutura de dados são: a remoção, que remove um elemento da estrutura; a inserção, que insere um novo elemento na estrutura; e a busca, que procura um elemento na estrutura a partir de parâmetros fornecidos. Aqui, o termo "elemento" é utilizado para referir-se a um dado da estrutura.
Um exemplo de estrutura muito utilizada é o vetor (array), onde os seus elementos são dispostos de forma linear e cada um deles possui um índice, que é um número inteiro que o identifica na estrutura. Assim, o acesso aos elementos do vetor é realizado por intermédio desses índices, em tempo constante.

Outro exemplo é a lista ligada simples. Na lista ligada, os elementos também são organizados de forma linear, entretanto eles são armazenados em estruturas mais simples, chamadas nós. Um nó possui um dado e um ponteiro (ou referência) para outro nó. Assim, um nó conecta-se a outro nó, que se conecta a outro e assim por diante. Portanto, se tivermos um nó, podemos acessar todos os nós subsequentes a ele. Observe que, ao contrário do vetor em que o acesso é realizado diretamente através dos índices, na lista ligada o acesso a um elemento ocorre percorrendo todos os elementos anteriores a ele.

O estudo de estruturas de estruturas de dados é fundamental para ciência da computação. Alguns algoritmos, por exemplo, só podem ser utilizados adequadamente em determinadas estruturas. Para ilustrar essa situação, vamos considerar o algoritmo de busca binária. Esse algoritmo permite realizar a busca de um elemento num vetor ordenado em tempo O(lg n), sendo mais rápido que a busca linear, que leva tempo O(n). Entretanto, a busca binária não poderia ser executada com a mesma eficiência numa lista ligada, justamente porque esse algoritmo se aproveita da propriedade do vetor de poder acessar qualquer um de seus elementos em tempo constante, através dos índices. Tal propriedade não existe na lista ligada.
Então o vetor é melhor que a lista ligada? Não necessariamente. O vetor possui algumas desvantagens críticas que torna o seu uso inviável, dependendo da situação. A primeira delas é que o vetor é uma estrutura de dados estática, ou seja, uma vez criado o seu tamanho não pode ser alterado. Ou seja, se um vetor estiver cheio e precisarmos de mais espaço para inserir elementos é necessário criar um novo vetor com um espaço maior, copiar todos os elementos do vetor antigo para o novo e inserir os novos elementos. Além disso, as operações de inserção e remoção num vetor podem requerer o deslocamento de elementos para posições à esquerda ou à direita. Em ambos os casos, haveria um grande custo em termos de memória e tempo de execução.
Por outro lado, a lista ligada é uma estrutura de dados dinâmica, ou seja, seu tamanho pode aumentar livremente, desde que não exceda a quantidade de memória disponível para a aplicação. Ao inserir um novo elemento, basta criar um novo nó com esse elemento e conectá-lo a algum nó da lista. Outra vantagem, é que as operações de inserção e de remoção não precisam realizar o deslocamento de elementos para a esquerda ou para a direita.
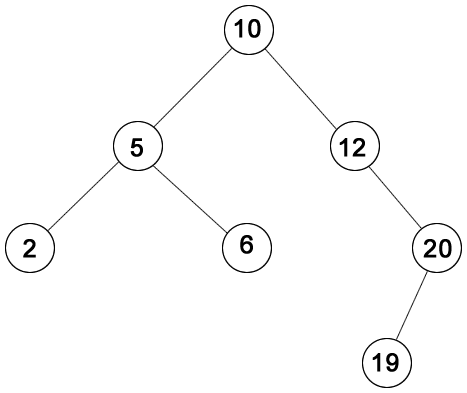
Vemos que a escolha da melhor estrutura depende muito da situação ou do problema considerado. Poderíamos nos deparar numa situação onde precisaríamos de uma estrutura que una as vantagens da busca binária do vetor e a alocação dinâmica de elementos da lista ligada. Uma possível solução seria utilizar a árvore de busca binária, que é uma estrutura de dados não linear, que também utiliza nós na sua estrutura e que dispõe os seus elementos de forma hierárquica.
Até agora, foram apresentadas brevemente algumas estruturas de dados e situações de uso, bem como suas vantagens e desvantagens. Entretanto, quando lidamos com uma estrutura de dados, a preocupação maior reside em descrever e compreender o seu funcionamento e suas operações, estabelecer regras e condições para que ela funcione corretamente, especificar o tempo de execução de cada uma de suas operações e custo no espaço (memória) para a alocação da estrutura.
Observe que não há uma preocupação direta com a implementação, pois a descrição abstrata é suficiente para que a estrutura seja implementada em alguma linguagem de programação. Na prática, estabelecemos um "contrato" que deve ser seguido para que a estrutura seja construída corretamente. Portanto, o que importa é que a estrutura funcione conforme o que foi estabelecido no contrato.
Alguns exemplos de estruturas de dados bem conhecidas são: filas, pilhas, heaps, árvores, tabelas de espalhamento (ou hash table) e listas ligadas. Cada uma possui, naturalmente, vantagens e desvantagens conforme a aplicação.
Por fim, estudar estruturas de dados é importante, pois com o avanço tecnológico ocorre um aumento na demanda por algoritmos e técnicas computacionais mais eficientes e, consequentemente, a introdução de estruturas de dados mais eficazes torna-se necessária. Além disso, com o surgimento de novos tipos de computação, como a computação quântica, novos tipos de estruturas precisam surgir, pois as estruturas clássicas podem não ser as mais adequadas nessas novas abordagens.
Referências
- CORMEN, T. H. et al. Algoritmos: teoria e prática. 3 ed. Tradução de Arlete Simille Marques. Rio de Janeiro: Elsevier, 2012.


Nenhum comentário:
Postar um comentário