Algoritmo Clássico de Multiplicação de Matrizes

Uma operação frequentemente utilizada na Matemática é a multiplicação de matrizes. Existe mais de um algoritmo que realiza essa operação, mas nesta postagem irei apresentar o algoritmo de multiplicação usual, que é ensinado no ensino médio (por isso coloquei "clássico" no título). Também disponibilizarei o algoritmo codificado na linguagem Java.

Revisão Rápida de Multiplicação de Matrizes

Por definição, o produto de matrizes AB só é possível se o número de colunas de A for igual ao número de linhas de B.

Por exemplo, o produto de matrizes a seguir não é possível, pois a primeira matriz tem 2 colunas e a segunda tem 3 linhas

Exemplo de multiplicação inválida

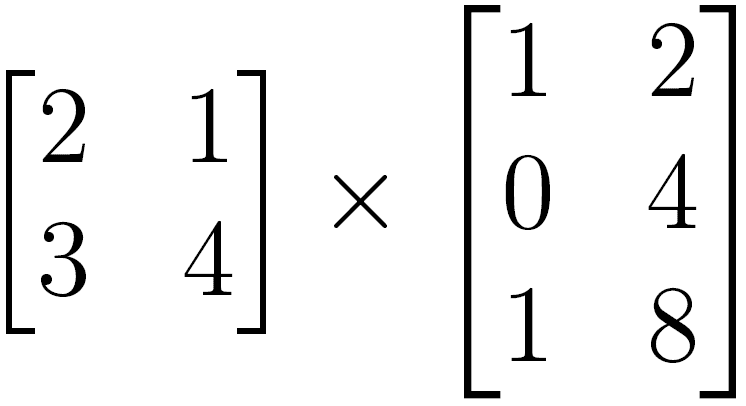
Por outro lado, o exemplo a seguir é possível, pois a definição é satisfeita

Exemplo de multiplicação válida

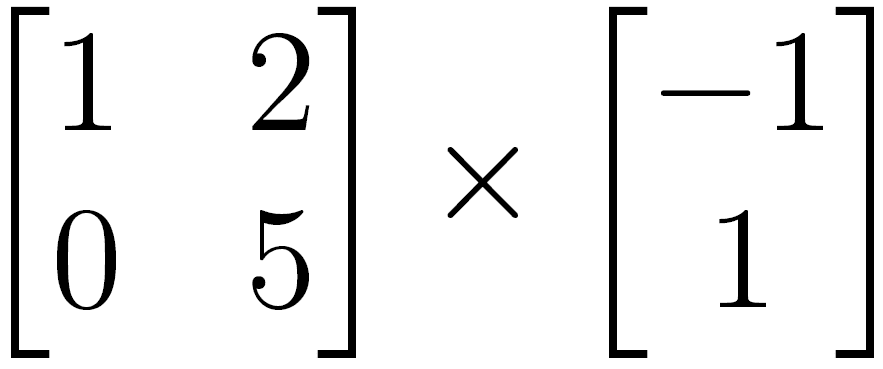
A matriz resultante terá o mesmo número de linhas da primeira matriz e o mesmo número de colunas da segunda matriz, isto é, A_{m × n} × B_{n × p} = C_{m × p}. No exemplo anterior, o resultado seria uma matriz com duas linhas e uma coluna.

Os elementos da matriz resultante são dados pela fórmula:

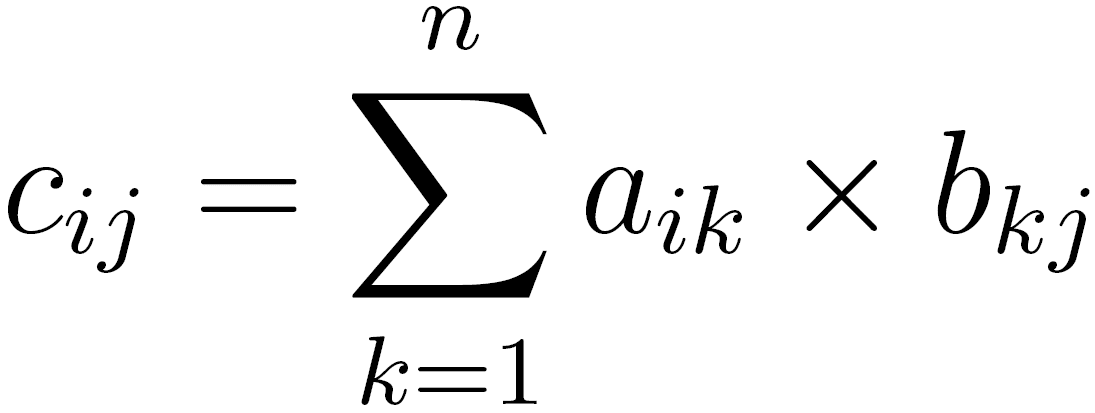
Isto é, o elemento da linha i e coluna j será a soma dos produtos dos elementos a_ik pelos elementos b_kj. A constante n é igual ao número de colunas da primeira matriz (que é igual ao número de linhas da segunda).

Um exemplo deixará mais claro. Vamos calcular o seguinte produto:

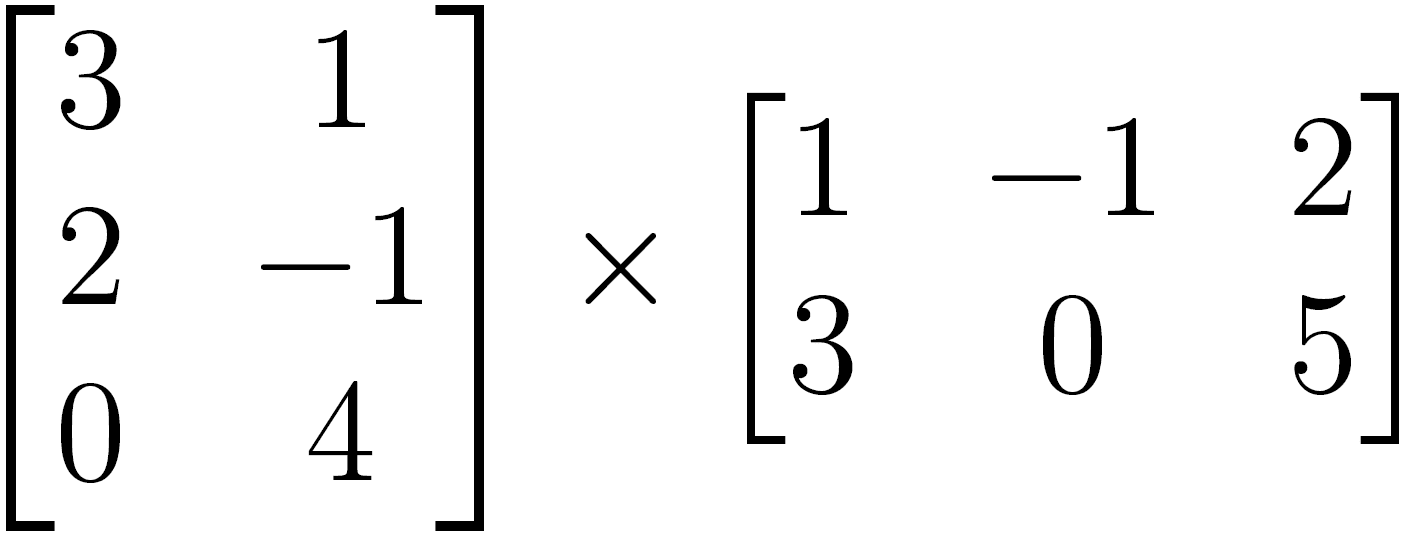
O resultado será uma matriz 3 × 3. Vamos calcular o primeiro elemento:

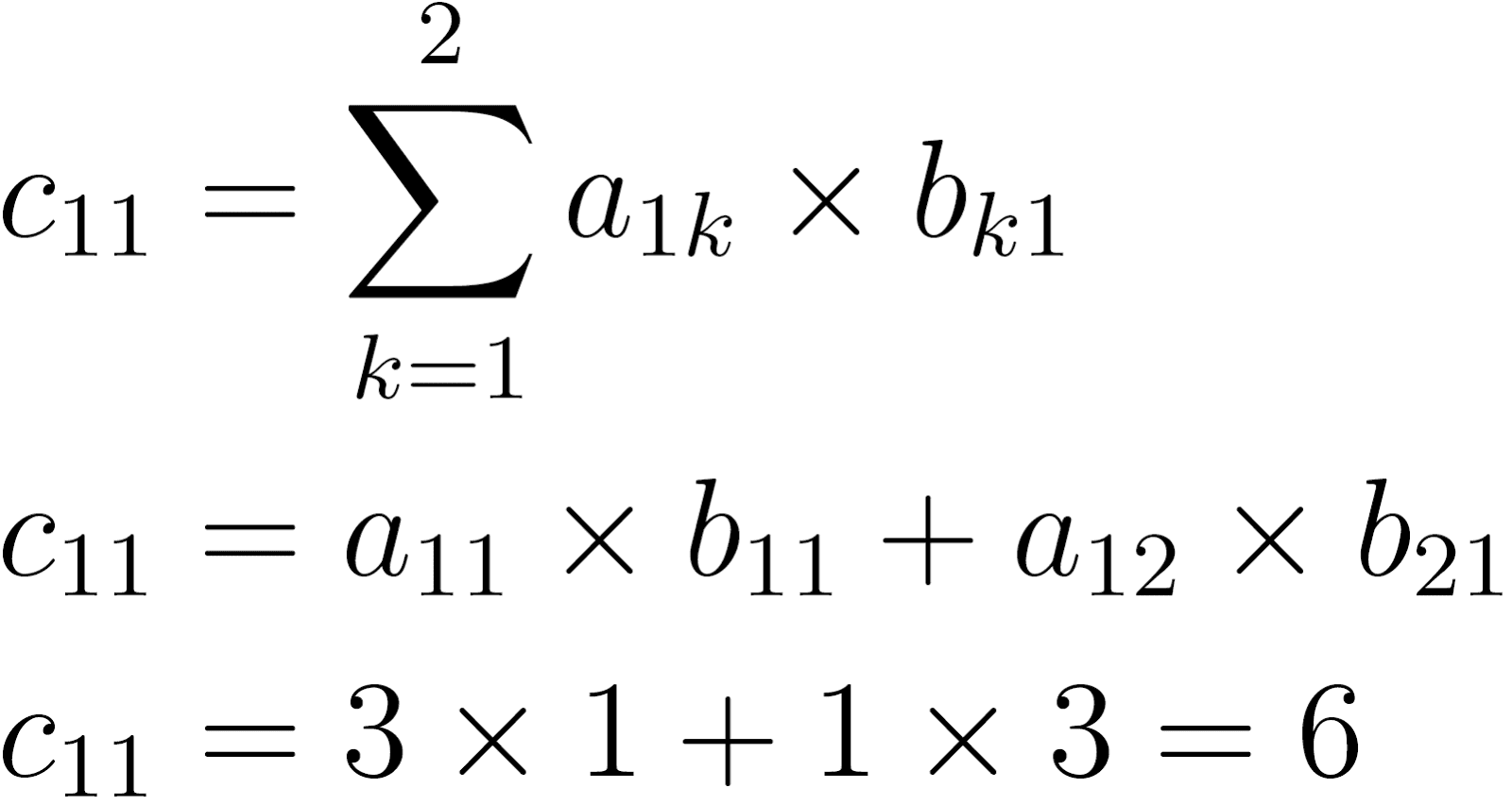
Ou seja, multiplicamos os elementos da linha i, da primeira matriz, pelos elementos correspondentes da coluna j, da segunda matriz, e somamos os resultados.

Repetindo o procedimento para todos os elementos, teremos

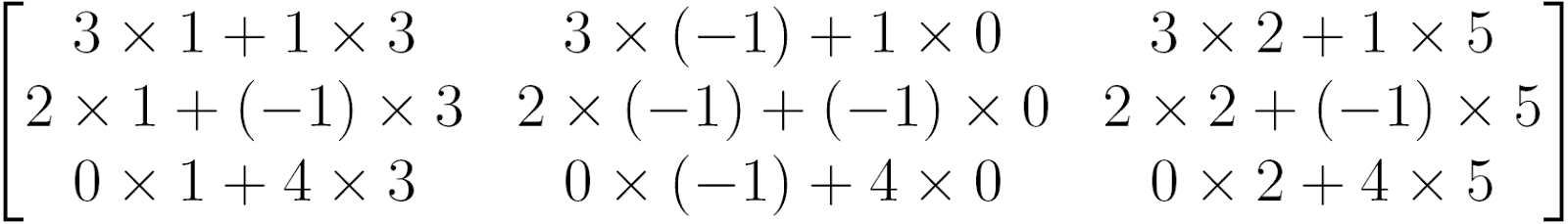
Que resulta em

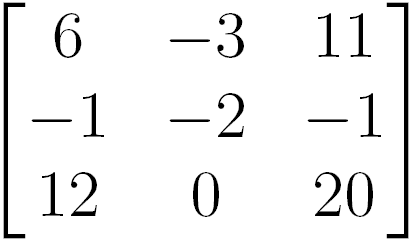
Construindo o Algoritmo

O primeiro passo é criar a matriz resultante. Tal matriz será uma matriz C_{m × p}, onde m é o número de linhas de A e p é o número de colunas de B.

multMatrix(Am × n, Bn × p)
      inicializar a matriz Cm × p
...     

Precisamos de um loop duplo aninhado para acessar cada posição da matriz C: um loop percorrerá as linhas e outro loop interno percorrerá as colunas (você pode inverter, se quiser):

multMatrix(Am × n, Bn × p)
      inicializar a matriz Cm × p
      para i ← 1 até m
            para j ← 1 até p
            ...
            fim_para
      fim_para
fim_multMatrix

Agora, basta aplicar a fórmula para calcular cada elemento c_ij. Observe que teremos mais um loop, pois precisaremos somar os produtos gerados pela multiplicação da filas de A e B (linhas e colunas, respectivamente). Ao final, obviamente, devemos retornar a matriz C. O algoritmo final em pseudocódigo é apresentado a seguir:

1. multMatrix(Am × n, Bn × p)
2.      inicializar a matriz Cm × p
3.      para i ← 1 até m
4.            para j ← 1 até p
5.                  para k ← 1 até n
6.                        Cij ← Cij + Aik × Bkj
7.                  fim_para
8.            fim_para
9.      fim_para
10.     retorne Cm × p
11. fim_multMatrix

Código em Java

A seguir, disponibilizo o algoritmo codificado em Java.

//Código por Henrique Felipe (GitHub: HenriqueIni)
public class MatrixMult {
    //Calcula A * B. A e B precisam ser matrizes válidas.
    //A.columns = B.rows
    public static double[][] mult(double[][] A, double[][] B){        
        int n = A[0].length; //A.columns = B.rows
        //Verfica se A.columns = B.rows
        if(n != B.length){
            throw new IllegalArgumentException("A.columns != B.rows");
        }
        int rows = A.length; //A.rows
        int cols = B[0].length; //B.columns
        double[][] C = new double[rows][cols];
        for(int i = 0; i < rows; i++){
            for(int j = 0; j < cols; j++){
                for(int k = 0; k < n; k++){
                    C[i][j] = C[i][j] + A[i][k] * B[k][j];
                }
            }
        }        
        return C;
    }
    //Método auxilar para converter uma matriz para String
    private static String toString(double[][] matrix){
        String aux = "";
        for(int i = 0; i < matrix.length; i++){
            aux += "[" + matrix[i][0];
            for(int j = 1; j < matrix[i].length; j++){
                aux += "," + matrix[i][j];
            }
            aux += "]";
            if(i != matrix.length - 1){
                aux += "\n";
            }
        }
        return aux;
    }
    //Testes
    public static void main(String[] args){
        //Exemplo 1        
        double[][] A = {{3, 1},
                        {2, -1},
                        {0, 4}};
        double[][] B = {{1, -1, 2},
                        {3, 0, 5}};
        System.out.println("A = \n" + toString(A));
        System.out.println("B = \n" + toString(B));
        System.out.println("A * B = \n" + toString(mult(A, B)));
        
        System.out.println();//break the line
        
        //Exemplo 2
        A = new double[][]{{1, 2},
                           {0, 5}};
        B = new double[][]{{-1},
                           {1}};
        System.out.println("A = \n" + toString(A));
        System.out.println("B = \n" + toString(B));
        System.out.println("A * B = \n" + toString(mult(A, B)));
    }
}

Análise

O triplo loop aninhado sugere que o algoritmo tem complexidade no tempo de O(m × p × n) ou ainda O(n³), se as matrizes forem quadradas de ordem n.

Na prática, é isso mesmo. O produto m × p × n é igual à quantidade de vezes que a linha 6 do pseudocódigo é executada.

Quando as matrizes são quadradas, existe um algoritmo, chamado de algoritmo de Strassen, que é ligeiramente mais eficaz, sendo capaz de realizar multiplicações de matrizes em tempo O(n^{lg 7}), onde lg 7 = log₂ 7 = 2,8... Entretanto, o algoritmo de Strassen não é intuitivo e sua implementação é complexa.

Referências

CORMEN, T. H. et al. Algoritmos: teoria e prática. 3 ed. Rio de Janeiro: Elsevier, 2012.