Questões do ENADE sobre Complexidade de Algoritmos #01

Nesta postagem, apresento a resolução de algumas questões do ENADE de Computação sobre Complexidade de Algoritmos. As questões são dos anos 2005 e 2008.

Para mais questões sobre o exame acesse a página ENADE.

ENADE 2005

As questões a seguir são do ENADE de 2005 de Computação.

Questão 13

Julgue os itens a seguir, acerca de algoritmos para ordenação.

• I) O algoritmo de ordenação por inserção tem complexidade $O(n \times \log n)$.
• II) Um algoritmo de ordenação é dito estável caso ele não altere a posição relativa de elementos de mesmo valor.
• III) No algoritmo quicksort, a escolha do elemento pivô influencia o desempenho do algoritmo.
• IV) O bubble-sort e o algoritmo de ordenação por inserção fazem, em média, o mesmo número de comparações.

Estão certos apenas os itens

• (A) I e II
• (B) I e III
• (C) II e IV
• (D) I, III e IV
• (E) II, III e IV

Resolução

A afirmativa I está errada, pois o algoritmo de ordenação por inserção (insertion sort) tem complexidade O(n²) no pior caso e no caso médio e O(n) no melhor caso. As demais afirmações estão corretas. Portanto, a alternativa correta é a (E).

Questão 15

Considere o algoritmo que implementa o seguinte processo: uma coleção desordenada de elementos é dividida em duas metades e cada metade é utilizada como argumento para a reaplicação recursiva do procedimento. Os resultados das duas reaplicações são, então, combinados pela intercalação dos elementos de ambas, resultando em uma coleção ordenada. Qual é a complexidade desse algoritmo?

• (A) $O(n^2)$
• (B) $O(n^{2n})$
• (C) $O(2^n)$
• (D) $O(\log n\times\log n)$
• (E) $O(n\times \log n)$

Resolução

O enunciado basicamente descreve o algoritmo de ordenação por intercalação (merge sort), cuja complexidade é $O(n\log n)$. Portanto, a alternativa correta é a (E).

Questão 43

No processo de pesquisa binária em um vetor ordenado, os números máximos de comparações necessárias para se determinar se um elemento faz parte de vetores com tamanhos 50, 1.000 e 300 são, respectivamente, iguais a

• (A) 5, 100 e 30.
• (B) 6, 10 e 9.
• (C) 8, 31 e 18.
• (D) 10, 100 e 30.
• (E) 25, 500 e 150.

Resolução

A busca binária requer cerca de log₂ n comparações para verificar se um elemento faz parte de um vetor de tamanho n:

log₂ 50 ≅ 5,6

log₂ 1000 ≅ 9,9

log₂ 300 ≅ 8,2

A alternativa que mais se aproxima desses resultados é a (B). Na prática, se você calcular o teto dos valores acima obterá os mesmos valores dessa alternativa (6, 10, 9).

É claro, na prova do ENADE não é permitido o uso de calculadoras. Nesse caso, você pode estimar o valor do logaritmo verificando o expoente das potências de 2 mais próximas de 50, 1.000 e 300, pois a base do logaritmo em questão é igual a 2:

32 < 50 < 64 ou 2⁵ < 50 < 2⁶

512 < 1000 < 1024 ou 2⁹ < 1000 < 2¹⁰

256 < 300 < 512 ou 2⁸ < 300 < 2⁹.

Analisando os expoentes, vemos que log₂ 50 está entre 5 e 6, log₂ 1000 está entre 9 e 10 e, finalmente, log₂ 300 está entre 8 e 9. Perceba que as estimativas estão de acordo com os resultados calculados anteriormente.

Por fim, concluímos que a alternativa (B) é a correta.

Questão 51

Imagem da questão 51 do ENADE 2005 de Computação

No famoso jogo da Torre de Hanoi, é dada uma torre com discos de raios diferentes, empilhados por tamanho decrescente em um dos três pinos dados, como ilustra a figura acima. O objetivo do jogo é transportar-se toda a torre para um dos outros pinos, de acordo com as seguintes regras: apenas um disco pode ser deslocado por vez, e, em todo instante, todos os discos precisam estar em um dos três pinos; além disso, em nenhum momento, um disco pode ser colocado sobre um disco de raio menor que o dele; é claro que o terceiro pino pode ser usado como local temporário para os discos.

Imaginando que se tenha uma situação em que a torre inicial tenha um conjunto de 5 discos, qual o número mínimo de movimentações de discos que deverão ser realizadas para se atingir o objetivo do jogo?

• (A) 25
• (B) 28
• (C) 31
• (D) 34
• (E) 38

Resolução

O problema da Torre de Hanói é um clássico no estudo de algoritmos recursivos (assim como o fatorial e a sequência de Fibonacci). O número de movimentações para n discos é calculado utilizando a fórmula 2ⁿ-1. Para 5 discos, o número mínimo de movimentações será 2⁵-1=31. Logo, a alternativa correta é a (C).

ENADE 2008

A questão abaixo é do ENADE 2008 de computação. Colocarei apenas uma para não estender a postagem.

Questão 18

Os números de Fibonacci constituem uma sequência de números na qual os dois primeiros elementos são 0 e 1 e os demais, a soma dos dois elementos imediatamente anteriores na sequência. Como exemplo, a sequência formada pelos 10 primeiros números de Fibonacci é: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34. Mais precisamente, é possível definir os números de Fibonacci pela seguinte relação de recorrência:

fib (n) = 0, se n = 0
fib (n) = 1, se n = 1
fib (n) = fib (n - 1) + fib (n - 2), se n > 1

Abaixo, apresenta-se uma implementação em linguagem funcional para essa relação de recorrência:

     fib :: Integer -> Integer
     fib 0 = 0
     fib 1 = 1
     fib n = fib (n - 1) + fib (n - 2)

Considerando que o programa acima não reutilize resultados previamente computados, quantas chamadas são feitas à função fib para computar fib 5?

Resolução

A maneira mais fácil de resolver a questão é construindo a árvore de recursão de fib(5) e contar quantos nós a árvore possui:

Clique na imagem para ampliar

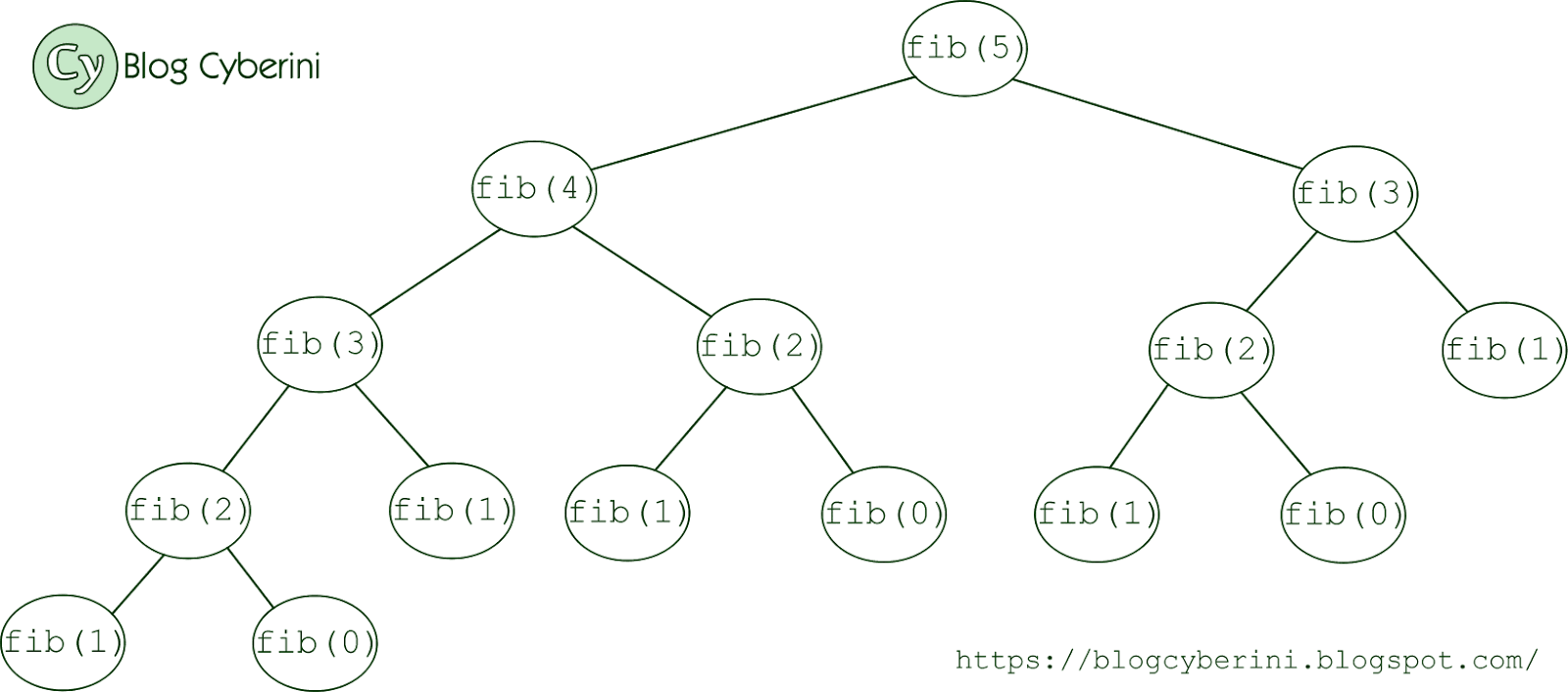
A árvore tem 15 nós, portanto fib 5 realiza 15 chamadas da função fib. Logo, a alternativa correta é a (C).