Nesta postagem, apresento a resolução de questões diversas do ENADE dos cursos de computação dos anos 2005 a 2014.

Para mais questões sobre o exame acesse a página ENADE.
ENADE 2005
As questões a seguir são do ENADE 2005 de computação.
Questão 21
No modo recursivo de representação, a descrição de um conceito faz referência ao próprio conceito. Julgue os itens abaixo, com relação à recursividade como paradigma de programação.
- I) São elementos fundamentais de uma definição recursiva: o caso-base (base da recursão) e a reaplicação da definição.
- II) O uso da recursão não é possível em linguagens com estruturas para orientação a objetos.
- III) As linguagens de programação funcionais têm, na recursão, seu principal elemento de repetição.
- IV) No que diz respeito ao poder computacional, as estruturas iterativas e recursivas são equivalentes.
- V) Estruturas iterativas e recursivas não podem ser misturadas em um mesmo programa.
Estão certos apenas os itens
- (A) I e IV.
- (B) II e III.
- (C) I, III e IV.
- (D) I, III e V.
- (E) II, IV e V.
Resolução
A afirmativa II é claramente falsa. Linguagens como C++, C# e Java são orientadas a objetos e suportam recursão, por exemplo.
A afirmativa V também é falsa. Ambas as estruturas podem ser utilizadas em conjunto. As demais afirmativas são verdadeiras. Logo, a alternativa correta é a C.
Questão 36
João, ao tentar consertar o módulo eletrônico de um carrinho de brinquedos, levantou as características de um pequeno circuito digital incluso no módulo. Verificou que o circuito tinha dois bits de entrada, x0 e x1, e um bit de saída. Os bits x0 e x1 eram utilizados para representar valores de inteiros de 0 a 3 (x0, o bit menos significativo e x1, o bit mais significativo). Após testes, João verificou que a saída do circuito é 0 para todos os valores de entrada, exceto para o valor 2.
Qual das expressões a seguir representa adequadamente o circuito analisado por João?
- (A) x0 and (not x1)
- (B) (not x0) or (not x1)
- (C) (not x0) and x1
- (D) x0 and x1
- (E) x0 or (not x1)
Resolução
O circuito em questão pode ser representado pela tabela da verdade a seguir
| x1 | x0 | Saída | |
| 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 2 | 1 | 0 | 1 |
| 3 | 1 | 1 | 0 |
A única expressão booleana que satisfaz a saída é $S = \overline{x_0}.x_1$, que também pode ser representada como S = (not x0) and x1. Portanto, a alternativa correta é a C.
ENADE 2008
A questão abaixo é do ENADE 2008 de computação. A questão é sobre circuitos digitais.
Questão 38
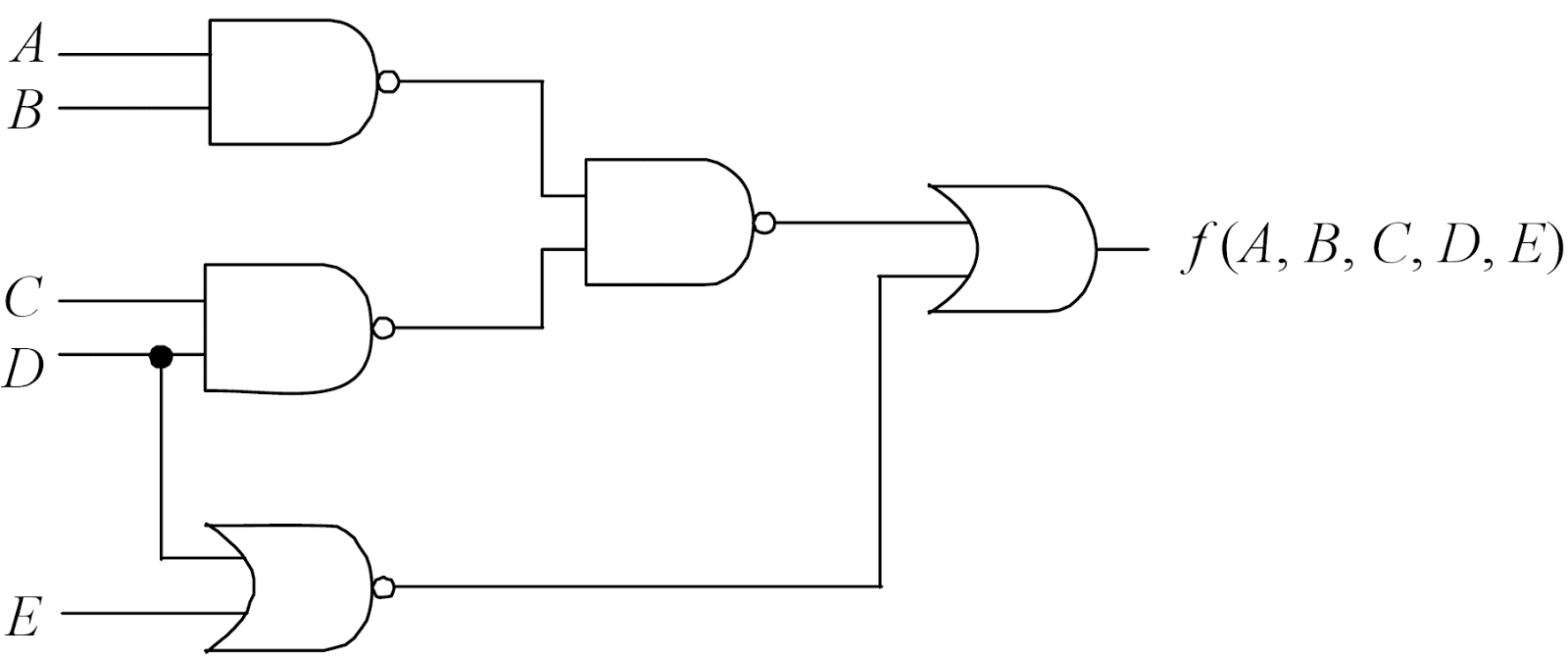
No circuito acima, que possui cinco entradas - A, B, C, D e E - e uma saída f(A, B, C, D, E), qual opção apresenta uma expressão lógica equivalente à função f(A, B, C, D, E)?
- (A) A.B + C.D + D.E
- (B) (A + B).(C + D) + D.E
- (C) A.B + C.D + D + E
- (D) A.B + C.D + D + E
- (E) A.B + C.D + D.E
Resolução
É conveniente analisar a saída de cada porta lógica e combiná-las uma a uma:
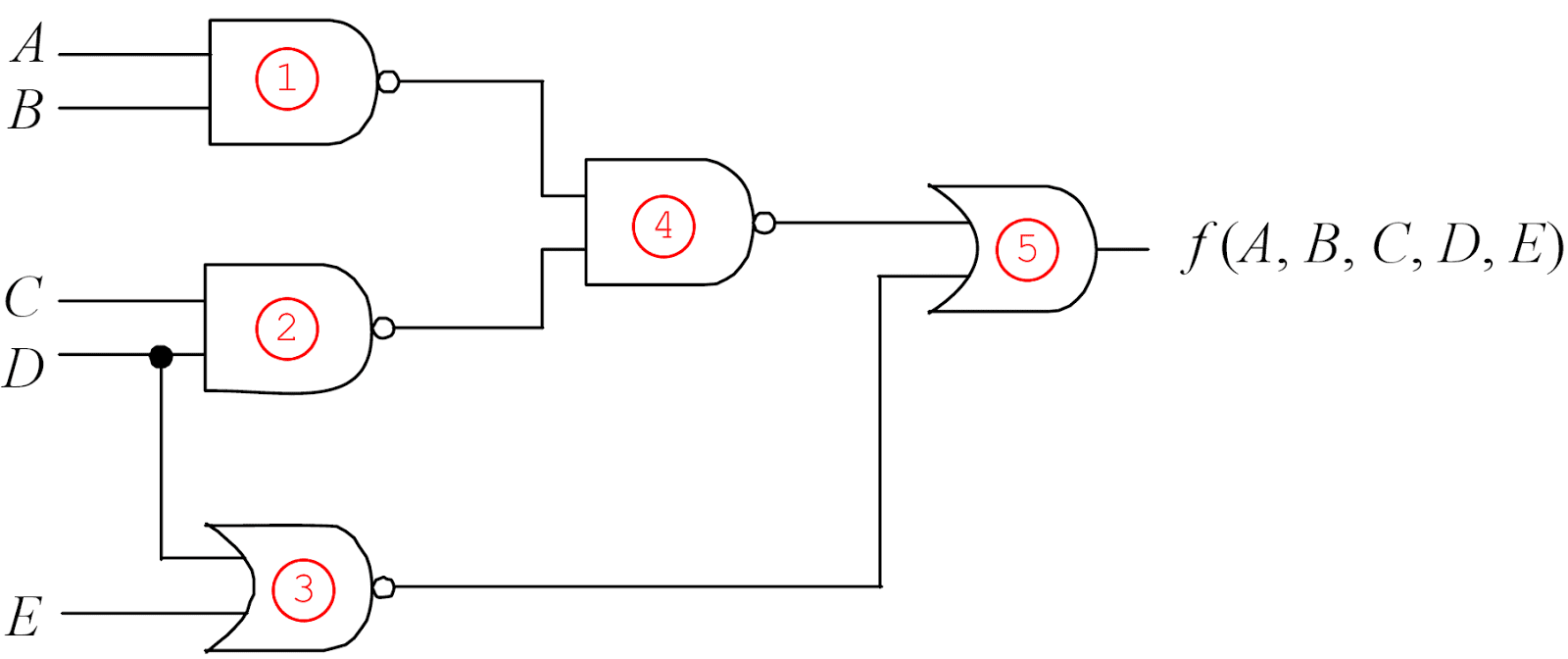
Para a porta 1, temos:

Porta 2:
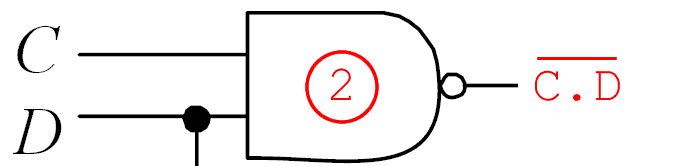
Porta 3:
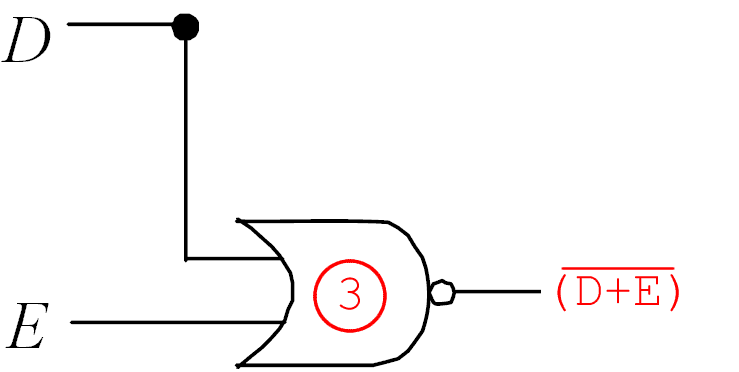
Porta 4:
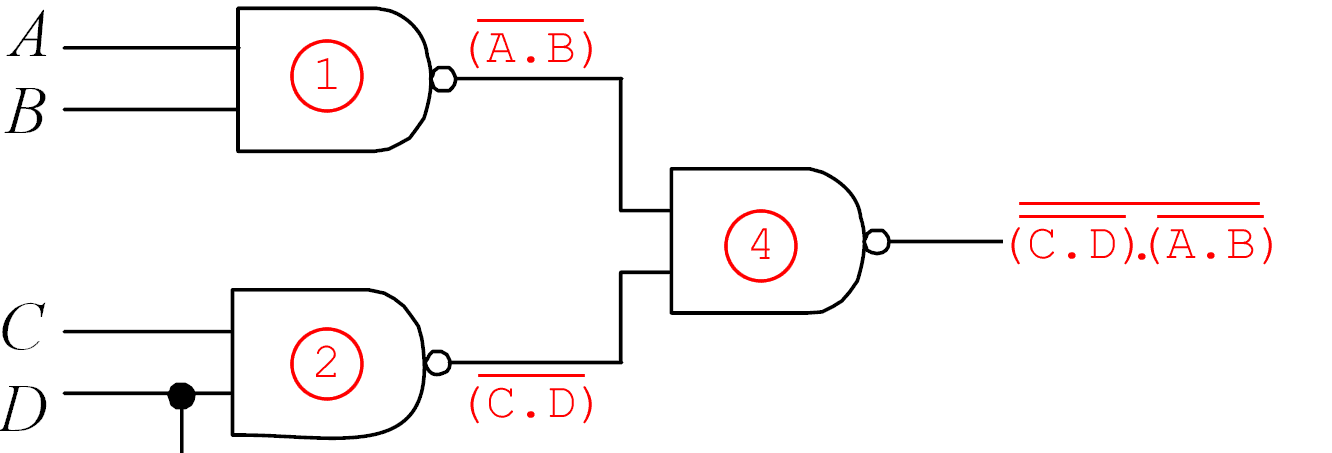
Os parênteses são apenas para dar ênfase. Combinando a saída da porta 3 com a saída da porta 4, obtém-se a saída do circuito completo:

Agora, basta simplificar a expressão utilizando o teorema de De Morgan:
$$\begin{align*}S &= \overline{(\overline{C.D}).(\overline{A.B})}+(\overline{D+E})\\&=(\overline{\overline{C.D}})+(\overline{\overline{A.B}})+\overline{D}.\overline{E}\\&=C.D+A.B+\overline{D}.\overline{E}\\&=A.B+C.D+\overline{D}.\overline{E}\end{align*}$$
Portanto, a expressão final é
f(A, B, C, D, E) = A.B + C.D + D.E.
Ou seja, a alternativa correta é a E.
ENADE 2011
As questões a seguir são do ENADE 2011 de computação.
Questão 19
Uma equipe está realizando testes com base nos códigos-fonte de um sistema. Os testes envolvem a verificação de diversos componentes individualmente, bem como das interfaces entre os componentes.
No contexto apresentado, essa equipe está realizando testes em nível de
- (A) unidade.
- (B) aceitação.
- (C) sistema e aceitação.
- (D) integração e sistema.
- (E) unidade e integração.
Resolução
A questão em si já dá a resposta. Enquanto o teste de componentes individuais corresponde ao nível de unidade, o teste das interfaces entre os componentes corresponde ao nível de integração. Ou seja, a alternativa E é a correta.
Questão 30
Suponha que se queira pesquisar a chave 287 em uma árvore binária de pesquisa com chaves entre 1 e 1000.Durante uma pesquisa como essa, uma sequência de chaves é examinada. Cada sequência abaixo é uma suposta sequência de chaves examinadas em uma busca da chave 287.
- I. 7, 342, 199, 201, 310, 258, 287
- II. 110, 132, 133, 156, 289, 288, 287
- III. 252, 266, 271, 294, 295, 289, 287
- IV. 715, 112, 530, 249, 406, 234, 287
É válido apenas o que se apresenta em
- (A) I.
- (B) III.
- (C) I e II.
- (D) II e IV.
- (E) III e IV.
Resolução
A sequência III está errada, pois todas as chaves depois da chave 294 deveriam ser maiores que ela. Após 294, o algoritmo de pesquisa visita o nó da chave 295, isto é, o filho direito. Nesse caso, todos os nós descendentes de 295 devem ser maiores que seu pai, ou seja, maiores de 294.
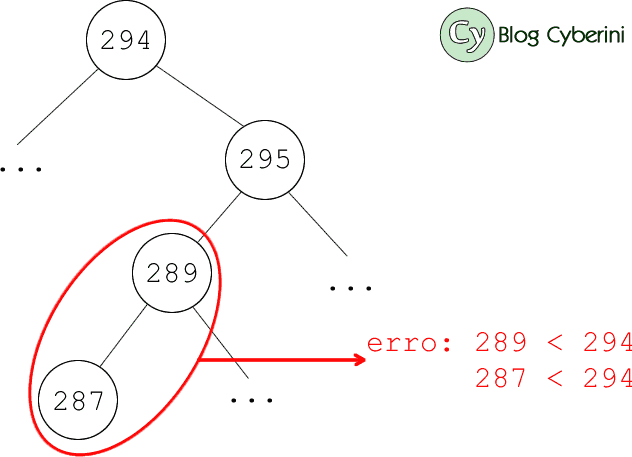
A sequência IV também está errada, pois todas as chaves depois da chave 249 deveriam ser maiores que ela, mas 234 é menor, o que viola as propriedades da árvore binária de pesquisa.
As demais sequências estão corretas, logo a alternativa C é a correta.
ENADE 2014
As questões a seguir são do ENADE 2014. Todas são da prova de Ciência da Computação.
Questão 13
A figura a seguir apresenta uma árvore binária de pesquisa, que mantém a seguinte propriedade fundamental: o valor associado à raiz é sempre menor do que o valor de todos os nós da subárvore à direita e sempre maior do que o valor de todos os nós da subárvore à esquerda.
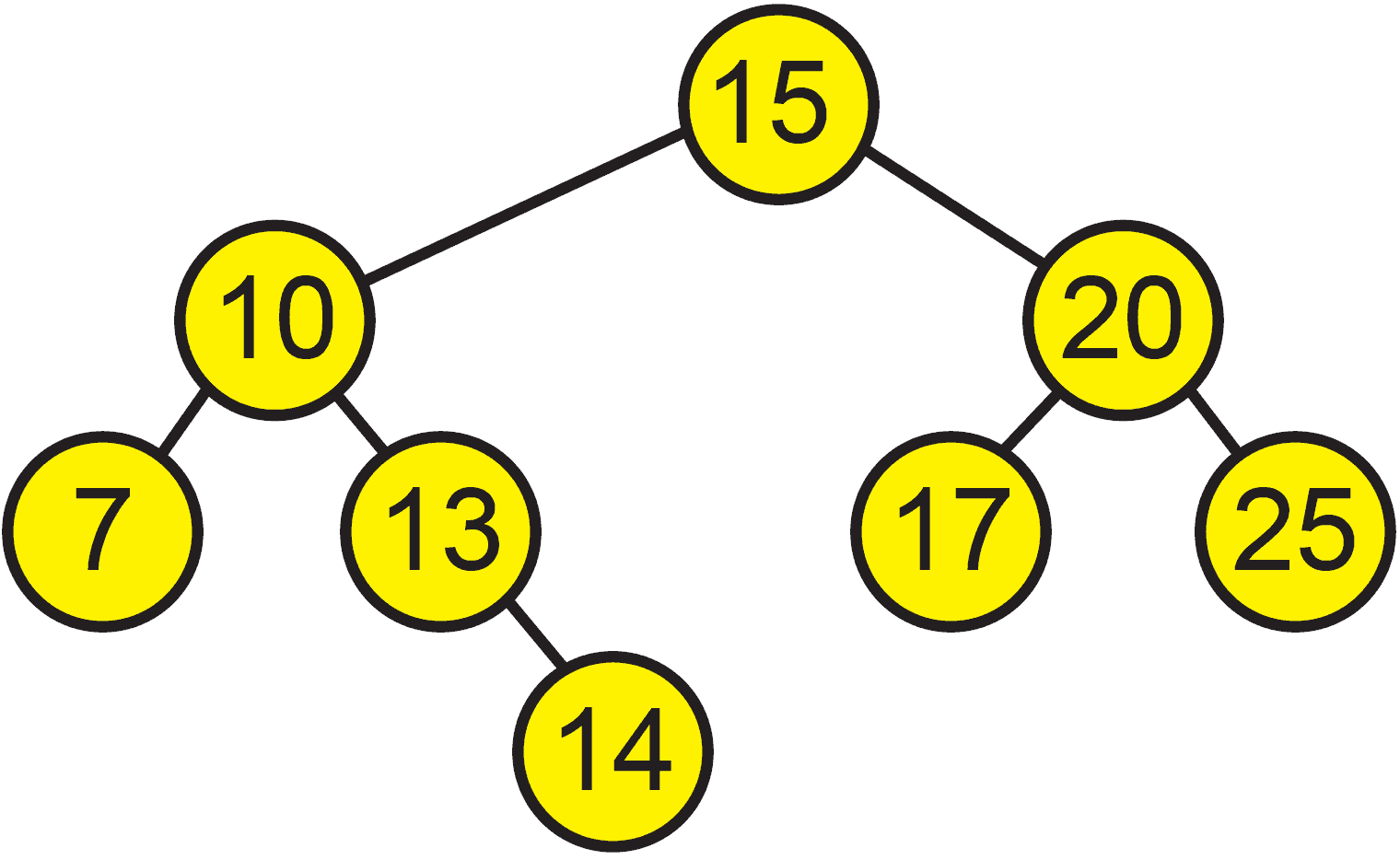
Em relação à árvore apresentada na figura, avalie as afirmações a seguir
- I. A árvore possui a vantagem de realizar a busca de elementos de forma eficiente, como a busca binária em um vetor.
- II. A árvore está desbalanceada, pois a subárvore da esquerda possui um número de nós maior do que a subárvore da direita.
- III. Quando a árvore é percorrida utilizando o método de caminhamento pós-ordem, os valores são encontrados em ordem decrescente.
- IV. O número de comparações realizadas em função do número n de elementos na árvore em uma busca binária realizada com sucesso é O(log n).
É correto apenas o que se afirma em
- (A) I e III.
- (B) I e IV.
- (C) II e III.
- (D) I, II e IV.
- (E) II, III e IV.
Resolução
A afirmação I está correta. Em ambos os casos, a complexidade é O(log n).
A afirmação II está incorreta. Em primeiro lugar, a árvore está balanceada (basta calcular os fatores de balanceamento dos nós para verificar isso). Em segundo lugar, não é a quantidade de nós que define o balanceamento e sim a altura das subárvores.
A afirmativa III está errada. O percurso em pós-ordem da árvore da questão é 7, 14, 13, 10, 17, 25, 20, 15, que obviamente não está em ordem decrescente.
A afirmação IV está correta. Portanto, a alternativa certa é a B.
Questão 14
Seja o universo $U=\{10,20,30,40\}$ e o conjunto dos números naturais N. Com base no conhecimento sobre lógica de predicados, avalie as afirmações a seguir.
- I. $H = (\forall x \in N)(\exists y \in U)(x<y)$ é válida.
- II. $H = (\forall x \in N)(\exists y \in N)(y<x)$ é válida.
- III. $H = (\forall x \in U)(\exists y \in U)(x>y)$ é inválida, sendo $x=10$ um contra-exemplo.
É correto o que se afirma em
- (A) I, apenas.
- (B) III, apenas.
- (C) I e II, apenas.
- (D) II e III, apenas.
- (E) I, II e III.
Resolução
A primeira afirmativa é falsa. Em português, a expressão significa "para todo x pertencente aos naturais, existe um y pertencente a U, tal que x < y". Qualquer valor de x a partir de 41 invalida a afirmação.
A afirmativa II também é falsa. Considerando que o menor número do conjunto dos números naturais seja o 0, se escolhermos x = 0, então a desigualdade y < x (ou, simplesmente, y < 0) sempre será falsa, pois não há natural menor do que zero.
Observação: algumas literaturas consideram o número 1 como menor/primeiro natural. Nesse caso, basta considerar x = 1.
A afirmativa III está correta. Portanto, a alternativa B é a correta.
Questão 16
Uma pilha é uma estrutura de dados que armazena uma coleção de itens de dados relacionados e que garante o seguinte funcionamento: o último elemento a ser inserido é o primeiro a ser removido. É comum na literatura utilizar os nomes push e pop para as operações de inserção e remoção de um elemento em uma pilha respectivamente. O seguinte trecho de código em linguagem C define uma estrutura de dados pilha utilizando um vetor de inteiros, bem como algumas funções para sua manipulação.
#include <stdlib.h>
#include <stdio.h>
typedef struct {
int elementos[100];
int topo;
}pilha;
pilha * cria_pilha() {
pilha * p =malloc(sizeof(pilha));
p->topo = -1;
return pilha;
}
void push(pilha *p, int elemento) {
if (p->topo >= 99)
return;
p->elementos[++p->topo] = elemento;
}
int pop(pilha *p) {
int a = p->elementos[p->topo];
p->topo--;
return a;
}
O programa a seguir utiliza uma pilha.
int main() {
pilha * p = cria_pilha();
push(p, 2);
push(p, 3);
push(p, 4);
pop(p);
push(p, 2);
int a = pop(p) + pop(p);
push(p, a);
a += pop(p);
printf("%d", a);
return 0;
}
A esse respeito, avalie as afirmações a seguir.
- I. A complexidade computacional de ambas funções
pushepopé O(1). - II. O valor exibido pelo programa seria o mesmo caso a instrução
a += pop(p);fosse trocada pora += a; - III. Em relação ao vazamento de memória (memory leak), é opcional chamar a função
free(p), pois o vetor usado pela pilha é alocado estaticamente.
É correto o que se afirma em
- (A) I, apenas.
- (B) III, apenas.
- (C) I e II, apenas.
- (D) II e III apenas.
- (E) I, II e III.
Observação: observe que há um erro na função cria_pilha(), que está retornando pilha ao invés de p.
Resolução
A afirmativa I está correta. As funções push e pop fazem a inserção e a remoção sempre no topo da pilha e, consequentemente, ambas as operações podem ser realizadas em tempo constante.
A afirmativa II também está correta. O valor de a e o valor de pop(p), após o comando push(p, a), são iguais a 5. Portanto, se trocássemos a instrução a += pop(p); por a += a;, o resultado do programa seria o mesmo.
A afirmativa III é falsa, pois a pilha foi alocada dinamicamente utilizando a função malloc, logo é necessário utilizar a função free para liberar a memória alocada.
Ou seja, a alternativa correta é a C.
Questão 23
Qual o valor de retorno da função a seguir, caso n = 27?
int recursao (int n) {
if (n <= 10) {
return n * 2;
}
else {
return recursao(recursao(n/3));
}
}
- (A) 8.
- (B) 9.
- (C) 12.
- (D) 16.
- (E) 18.
Resolução
Para n = 27:
recursao(27) = recursao(recursao(27/3)) = recursao(recursao(9))
Como 9 <= 10, então recursao(9) = 2 * 9 = 18:
recursao(27) = recursao(18) = recursao(recursao(6))
Como 6 <= 10, então recursao(6) = 2 * 6 = 12
recursao(27) = recursao(12) = recursao(recursao(4))
Como 4 <= 10, então recursao(4) = 2 * 4 = 8
recursao(27) = recursao(8)
Como 8 <= 10, então recursao(8) = 2 * 8 = 16. Por fim,
recursao(27) = 16
Portanto, a alternativa correta é a D.

Nenhum comentário:
Postar um comentário