Questões do POSCOMP sobre Linguagens Formais e Autômatos #03

Nesta postagem, apresento algumas questões resolvidas do POSCOMP dos anos 2008 e 2009 sobre Linguagens Formais e Autômatos.

Se as fórmulas matemáticas não aparecerem ou ficarem estranhas, recarregue a página. Se o problema persistir, por favor, deixe um comentário para que eu possa averiguar o problema ou preencha o formulário de contato.

Leia também: Aplicativos para Estudar para o POSCOMP

POSCOMP 2008

As questões a seguir são do ano 2008.

Questão 43

Considere o autômato finito mostrado na figura abaixo (os círculos em negrito representam estados terminais).

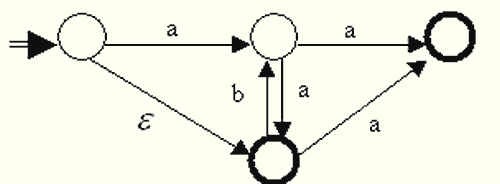
A esse respeito, assinale a afirmativa FALSA.

• (A) A palavra aaa é reconhecida pelo autômato.
• (B) A palavra ababa não é reconhecida pelo autômato.
• (C) A palavra vazia é reconhecida pelo autômato.
• (D) A palavra aba é reconhecida pelo autômato.
• (E) A palavra baba é reconhecida pelo autômato.

Resolução

A questão é fácil. A única afirmativa falsa é a D. Após reconhecer o primeiro a da cadeia aba, não é possível reconhecer o b. Portanto, a cadeia aba não é reconhecida pelo autômato.

Questão 44

Considere a seguinte gramática $G$, onde $S$ é o símbolo inicial:

$$\begin{align*}S&\rightarrow AcB\\A&\rightarrow cA\,|\,aB\\B&\rightarrow cB\,|\,aA\\A&\rightarrow \varepsilon\end{align*}$$

Assinale a alternativa que apresenta a palavra que NÃO pertence à linguagem gerada pela gramática $G$.

• (A) ccca
• (B) aaca
• (C) aaaca
• (D) ccac
• (E) aaa

Resolução

Observe que toda cadeia gerada pela gramática G deve conter pelo menos um c ($S\rightarrow AcB$). A única cadeia que não contém c é a cadeia aaa da alternativa E, que é a opção correta.

Questão 45

Considere as seguintes gramáticas.

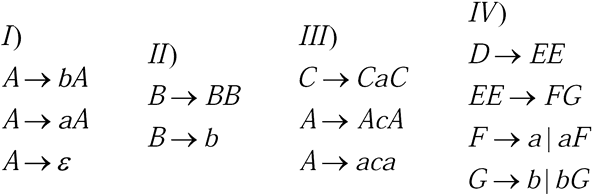
A esse respeito, assinale a afirmativa FALSA.

• (A) A gramática I é livre de contexto.
• (B) A gramática II é livre de contexto.
• (C) A gramática III é livre de contexto.
• (D) A gramática IV é livre de contexto.
• (E) Nenhuma das gramáticas é livre de contexto.

Resolução

Para resolver esta questão, basta saber quais gramáticas são livres de contexto e quais não são.

A gramática I é regular, portanto também é livre de contexto.

As gramáticas II e III são livres de contexto.

A gramática IV é sensível ao contexto por causa da produção $EE\rightarrow FG$, que a torna a única gramática que não é livre de contexto.

Portanto, a afirmativa falsa é a D.

Questão 46

Seja o autômato finito mostrado na figura abaixo que opera sobre o alfabeto $\Sigma=\{a,b\}$ (o círculo em negrito indica um estado terminal):

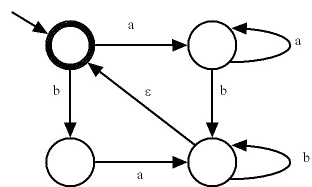
Analise as seguintes afirmativas.

• I. O autômato finito mostrado na figura é determinístico.
• II. O autômato finito mostrado na figura é não-determinístico.
• III. O autômato finito mostrado na figura reconhece a palavra vazia.

A análise permite concluir que

• (A) todas as afirmativas são falsas.
• (B) somente a afirmativa I é falsa.
• (C) somente a afirmativa II é falsa.
• (D) somente a afirmativa III é falsa.
• (E) nenhuma das afirmativas é falsa.

Resolução

A afirmação I é falsa, pois autômatos finitos determinísticos não possuem transições vazias.

A afirmação II é verdadeira porque o autômato possui uma transição vazia.

A afirmativa III também é verdadeira, pois o estado inicial do autômato também é um estado final, logo ele reconhece a palavra vazia.

Portanto, a alternativa correta é a B.

POSCOMP 2009

A questão a seguir é do ano 2009.

Questão 35

Seja o alfabeto $\Sigma=\{a,b\}$ e a linguagem regular

$$L=\{\omega\,|\,\omega\in\Sigma^{*}\text{ e o nº de a's em }\omega\text{ é par}\}.$$

Qual das expressões regulares abaixo gera essa linguagem?

• (A) $(a\,b^{*}\,a\,b^{*})^{*}$
• (B) $((a\,a)^{*}\,|\,b^{*})^{*}$
• (C) $(b^{*}\,|\,(a\,a)^{*}\,|\,b^{*})^{*}$
• (D) $(b^{*}a\,b^{*}a\,b^{*})^{*}$
• (E) $(aa\,|\,b)^{*}$

Resolução

Na prática, todas as alternativas estão incorretas.

A expressão regular (ER) em A não reconhece a cadeia baba, que possui um número par de a's.

As ERs em B e C são equivalentes:

$$\begin{align*}(b^{*}|(aa)^{*}|b^{*})&=((aa)^{*}|b^{*}|b^{*})\\&=((aa)^{*}|b^{*})\end{align*}$$

Lembre-se: se $\alpha$ é uma ER, então $\alpha|\alpha=\alpha$. Além disso, o operador de união "|" é comutativo.

Entretanto, as expressões regulares em B e em C também não reconhecem a cadeia baba.

A ER em E também não reconhece a cadeia baba.

Por fim, a nossa salvação seria a expressão regular da alternativa D. Mas ela está errada porque não reconhece cadeias sem a's (zero é par), tal como a cadeia bb. A expressão regular que gera L é

$$(b^{*}ab^{*}ab^{*})^{*}|b^{*}$$

Essa ER é praticamente igual à ER em D, porém sem o problema apresentado.

Conforme o gabarito oficial, a alternativa "correta" é a D. Na prática, é a alternativa mais próxima de estar correta, mas não está.

Postagens Relacionadas

Questões do POSCOMP sobre Complexidade de Algoritmos #01

Questões do POSCOMP sobre Linguagens Formais e Autômatos #02

Acesse a tag POSCOMP do blog para ver mais postagens sobre a prova.