Questões do POSCOMP sobre Linguagens Formais e Autômatos #04

Nesta postagem, apresento algumas questões resolvidas do POSCOMP dos anos 2009, 2012, 2013, 2015 e 2016 sobre Linguagens Formais e Autômatos.

Se as fórmulas matemáticas não aparecerem ou ficarem estranhas, recarregue a página. Se o problema persistir, por favor, deixe um comentário para que eu possa averiguar o problema ou preencha o formulário de contato.

Leia também: Aplicativos para Estudar para o POSCOMP

POSCOMP 2009

As questões a seguir são do ano 2009.

Questão 45

Considere o autômato finito não-determinístico a seguir, sendo A o estado inicial e D o único estado de aceitação.

Autômato da questão 45 do POSCOMP 2009

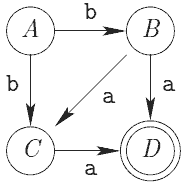
Que autômato finito determinístico com d como sua função de transição de estado aceita a mesma linguagem?

• (A)
  Estado Inicial A, estados de aceitação C e D
  d(A, b) = B
  d(B, a) = C
  d(C, a) = D
• (B)
  Estado Inicial A, estado de aceitação C
  d(A, b) = B
  d(B, a) = C
  d(C, a) = C
• (C)
  Estado Inicial A, estado de aceitação D
  d(A, b) = B
  d(B, a) = D
  d(B, b) = C
  d(C, a) = D
• (D) Todas as respostas acima estão corretas.
• (E) É impossível converter esse autômato finito não determinístico em um autômato finito determinístico.

Resolução

Primeiramente, observe que o autômato reconhece apenas duas cadeias, que formam uma linguagem finita: ba e baa. Isso elimina a alternativa B, pois a transição $d(C, a)=C$ gera um laço, portanto, a linguagem reconhecida pelo autômato em B é infinita.

Uma vez que B é falsa, então a alternativa D é automaticamente falsa.

A alternativa E também é falsa, pois qualquer AFND pode ser convertido em um AFD, pois as duas classes de autômatos são equivalentes.

O autômato em C reconhece a linguagem L = {ba, bba}, que é diferente da linguagem do autômato da questão. Logo, a alternativa C está errada.

A única alternativa correta é a A. O autômato de A é representado a seguir.

Autômato da alternativa A

Questão 56

Qual é a linguagem da gramática com as seguintes regras de produção

$$\begin{align*}S&\rightarrow ASb\,|\,c\\A&\rightarrow a\end{align*}$$

• (A) $\{a^ncb\,|\,n\in\mathbb{N}\}$
• (B) $\{acb^n\,|\,n\in\mathbb{N}\}$
• (C) $\{a^nc^nb\,|\,n\in\mathbb{N}\}$
• (D) $\{a^ncb^n\,|\,n\in\mathbb{N}\}$
• (E) Nenhuma das respostas anteriores

Resolução

A gramática pode ser simplificada

$$S\rightarrow aSb|c$$

Para cada a à esquerda, teremos um b à direita e, no meio, temos um c:

$$L=\{c,acb,aacbb,aaacbbb,\ldots\}$$

Portanto, a alternativa correta é a D.

POSCOMP 2012

A questão a seguir é de 2012.

Questão 41

Seja um Autômato Finito Não Determinístico (AFN) com 6 estados. Aplicando-se o algoritmo de conversão de um AFN para um Autômato Finito Determinístico (AFD), em quantos estados, no máximo, resultaria o AFD considerando-se os estados inúteis?

• (A) 12
• (B) 36
• (C) 64
• (D) 1024
• (E) 46656

Resolução

O cálculo é simples. Basta calcular 2 elevado ao número de estados do AFN:

$$2^6=64\text{ estados}$$

Portanto, a alternativa C é a correta.

POSCOMP 2013

A questão a seguir é de 2013.

Questão 41

Se o estado inicial for também estado final em um autômato finito, então esse autômato

• (A) não aceita a cadeia vazia.
• (B) não tem outros estados finais.
• (C) é determinístico.
• (D) aceita a cadeia vazia.
• (E) é não determinístico.

Resolução

A questão é fácil. Quando o estado inicial também é final num AF, então ele aceita a cadeia vazia. Logo, a opção certa é a D.

POSCOMP 2015

As questões a seguir são do ano 2015.

Questão 39

A gramática $G = (\{S, A, B\}, \{0, 1\}, P, S)$, onde $P$ é dado pelas regras de produção

$$\begin{align*}S&\rightarrow 0AB\,|\,1BA\\A&\rightarrow 0AS\,|\,1A\,|\,\varepsilon\\B&\rightarrow 0B\,|\,1BS\,|\,\varepsilon\end{align*}$$

gera uma linguagem que

• (A) pertence à classe Regular.
• (B) contém a cadeia vazia $\varepsilon$
• (C) pode ser aceita por um autômato com pilha.
• (D) pode ser denotada por uma expressão regular.
• (E) é igual ao conjunto de cadeias {x ∈ {0, 1}* | x tem quantidade igual de zero (0) e de um (1)}}

Resolução

$G$ é uma gramática livre de contexto que, consequentemente, gera uma linguagem livre de contexto. Toda linguagem livre de contexto pode ser reconhecida por um autômato com pilha.

Portanto, a alternativa correta é a C.

Questão 40

Considerando as linguagens $L =\{0^n1^n2^i\,|\,n \geq 0\,e\,i\geq 0\}$ e $M =\{0^i1^n2^n\,|\,n \geq 0\,e\,i\geq 0\}$, pode-se afirmar que

• (A) a linguagem $L\cup M$ pode ser gerada por uma gramática livre de contexto.
• (B) a linguagem M pode ser gerada por uma gramática regular.
• (C) a linguagem L pode ser aceita por um autômato finito determinístico.
• (D) a linguagem $L\cap M$ pertence à classe das linguagens livres de contexto.
• (E) a linguagem M pode ser denotada por uma expressão regular.

Resolução

As duas linguagens são livres de contexto, por causa da "simetria" relacionada à variável $n$. Assim, essas linguagens só podem ser geradas por gramáticas livres de contexto. Só isso já descarta as alternativas B, C e E.

A alternativa D é falsa, pois a linguagem $L\cap M$ é representada por $0^n1^n2^n$, que não pode ser gerada por uma gramática livre de contexto. Portanto, $L\cap M$ não é livre de contexto. Na prática, essa linguagem é sensível ao contexto.

A alternativa A está correta. Uma gramática livre de contexto capaz de gerar $L\cup M$ é representada a seguir

$$G=\left(\{S,A,B,C,D\},\{0,1\},P,S\right)$$

$$\begin{align*}S&\rightarrow AB|CD\\A&\rightarrow 0A1|\lambda\\B&\rightarrow 2B|\lambda\\C&\rightarrow 0C|\lambda\\D&\rightarrow 1D2|\lambda\end{align*}$$

POSCOMP 2016

A questão a seguir é de 2016.

Questão 39

O grafo rotulado G(r), exposto abaixo, representa qual expressão regular?

Autômato/grafo da questão 39 do POSCOMP 2016

• (A) $r=ab^{*}(da^{*}+cb)^{*}$
• (B) $r=a^{*}b(d^{*}+cb)$
• (C) $r=(bb+d)^{*}(aa+c)^{*}$
• (D) $r=a^{*}b(c+da^{*}b)^{*}$
• (E) $r=a^{*}c^{*}(b+d)^{*}$

Resolução

Partindo do estado inicial, podemos gerar 0 (zero) ou mais a's e, em seguida, gerar um b, mudando para o estado final. Ou seja, a expressão regular deve iniciar com $a^{*}b$. Isso elimina as alternativas A, C e E.

Depois, podemos simplesmente parar no estado final ou gerar combinações de c's ou $da^{*}b$. Isto é, $\left(c|da^{*}b\right)^{*}$. Combinando as expressões, obtemos a expressão regular completa, que é $a^{*}b\left(c|da^{*}b\right)^{*}$. Portanto, a alternativa correta é a D.

Observação: o operador "+" é o operador de união "|". A notação "+" para esse operador é pouco comum (os elaboradores do POSCOMP costumam utilizá-la nas provas).

Postagens Relacionadas

Questões do POSCOMP sobre Complexidade de Algoritmos #01

Questões do POSCOMP sobre Linguagens Formais e Autômatos #03

Acesse a tag POSCOMP do blog para ver mais postagens sobre a prova.