Como verificar se um número é par ou ímpar?

Por mais boba que a pergunta do título desta postagem pareça, ela é frequente entre aqueles que estão aprendendo a programar, sendo tópico de fóruns e até de discussões no StackOverflow.

Por isso, nesta postagem apresento duas formas de verificar se um número é par ou ímpar.

Primeira forma: resto da divisão

Um número inteiro é par quando é divisível por 2, isto é, o resto da divisão por 2 é zero

Se um número não é par, então ele é ímpar. Isto é, o resto da divisão por 2 não é zero.

Na maioria das linguagens de programação, o resto da divisão pode ser calculado diretamente através do operador % (mod)

12 % 2 = 0

13 % 2 = 1

Portanto, você pode verificar se um número é par utilizando a seguinte condição (Java, C, C++, Javascript, Blogger, etc.)

(n % 2) == 0

Essa condição retornará true se n for par e false se n for ímpar. Num clássico if...else, teríamos

if((n % 2) == 0){
   //n é par
}else{
   //n é ímpar
}

Esse método é o mais utilizado para checar a paridade de um número e também é o mais intuitivo.

Segunda forma: operador bitwise AND

O segundo método que irei apresentar utiliza um operador bit-a-bit pouco conhecido, portanto irei apresentá-lo rapidamente antes de explicar esse método.

O operador bitwise AND (E binário/E sobre bits/E bit-a-bit) é um operador binário que opera diretamente sobre os bits de seus operandos e é normalmente denotado pelo símbolo &.

Basicamente, ele aplica a operação lógica AND nos bits correspondentes dos operandos. Como exemplo, vamos calcular 11 & 6

11 = (1011)2 e 6 = (110)2

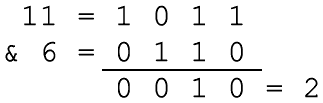
Logo, 11 & 6 = (10)2 = 2.

Podemos verificar se um número é par com o operador bitwise AND através da expressão

(n & 1) == 0

Esse método explora o fato de que todo número par em binário tem bit mais à direita igual a zero. Já os números binários ímpares têm bit mais à direita igual a 1. Entretanto, existe uma exceção que explicarei depois.

Se n é par, então n & 1 = 0. Se n é ímpar, então n & 1 = 1

A vantagem desse método é que, em geral, as operações sobre bits são mais rápidas que as operações aritméticas. Porém, esse método não é intuitivo.

Além disso, o funcionamento desse método só é garantido para números não negativos (essa é a exceção). Isso ocorre por causa da maneira como as linguagens de programação representam os números inteiros.

Se a linguagem que você trabalha não utiliza a representação complemento de dois na representação de números inteiros, então o bit mais à direita em números binários negativos não necessariamente será 0 para os pares e 1 para os ímpares.

As linguagens de programação Java [3], JavaScript [1] e Python [2], por exemplo, utilizam a representação complemento de dois (consulte as referências no final do artigo para maiores informações), logo esse método funcionará nessas linguagens mesmo com números negativos.

Eu tentei pesquisar se outras linguagens famosas também utilizam essa representação, mas não consegui informações de fontes confiáveis, por isso não as listei.

Considerações Finais

Apesar do método envolvendo o operador bitwise AND ser, em geral, mais rápido, devemos lembrar que a operação mod % é frequentemente utilizada pelos programadores (não apenas para checar a paridade de um número), logo é de se esperar que os compiladores realizem algum tipo de otimização para que essa operação consuma menos ciclos de processamento que o normal.

Referências

[1] W3Schools. JavaScript Bitwise Operations.

[2] Python Documentation. 3. Data model.

[3] The Java™ Tutorials. Primitive Data Types.