Nesta postagem, apresento a resolução de algumas questões do POSCOMP 2002. As questões são da parte de "Fundamentos" do exame.
Esta é a primeira parte das soluções, pois posteriormente eu pretendo fazer mais publicações.
Índice
Para mais questões resolvidas, acesse a página POSCOMP.
Questão 21
Assunto: arquitetura de computadores (índice).
Uma característica de uma arquitetura RISC é
- (A) Uma arquitetura de alto risco pois o mercado de hardware evolui muito rapidamente
- (B) Possui um grande conjunto de instruções complexas
- (C) A arquitetura é constituída de milhares de processadores
- (D) Possui um pequeno conjunto de instruções simples
- (E) O processador é formado por válvulas e transistores
Resolução
A principal característica da arquitetura RISC é que os processadores possuem um conjunto reduzido de instruções simples, algo que permite mais velocidade e menor consumo de energia.
RISC significa Reduced Instruction Set Computer, isto é, Computador com um Conjunto Reduzido de Instruções. Portanto, a alternativa correta é a D.
Aliás, os principais pesquisadores por trás da arquitetura RISC receberam o Prêmio Turing 2017 por suas contribuições.
Questão 22
Assunto: circuitos digitais/lógica (índice).
Na Álgebra Booleana
- (A) Os dígitos são octais, de 0 a 7
- (B) Os dígitos são binários 0 e 1
- (C) Há dez valores motivados pelos dez dedos do ser humano
- (D) Os dígitos são alfanuméricos que podem ser representados por um byte
- (E) Os dígitos são hexadecimais de 0 a 15
Resolução
Na Álgebra Booleana, trabalhamos com dois valores, que podem ser F ou V ou, respectivamente, 0 ou 1. Ou seja, os dígitos são binários.
Portanto, a alternativa correta é a B.
Questão 23
Assunto: circuitos digitais (índice).
Considere o circuito abaixo, implementado com duas portas NAND.
Qual das seguintes portas equivale a este circuito?
- (A)
NOT - (B)
OR - (C)
AND - (D)
XOR - (E)
NOR
Resolução
A saída do circuito é representada a seguir
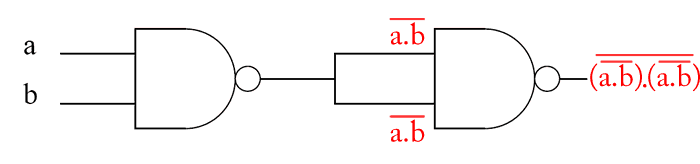
Agora, vamos simplicar a expressão
$$\begin{align*}S&=\overline{(\overline{a.b}).(\overline{a.b})}\\&=\overline{(\overline{a.b})}\\&=a.b\end{align*}$$
Ou seja, após as simplificações, concluímos que o circuito é equivalente a uma porta AND. Portanto, a alternativa correta é a C.
Questão 24
Assunto: circuitos digitais (índice).
Considere o projeto de um circuito digital que implementa uma função $f$ com três variáveis de entrada e satisfazendo as seguintes propriedades:
$$f(x,y,z)=\begin{cases}1&\mbox{se }x\neq y\\0&\mbox{caso contrário}\end{cases}$$
Qual das seguintes expressões representa corretamente a função $f$?
- (A) $x+\overline{y}z$
- (B) $\overline{xyz}+x\overline{y}z$
- (C) $\overline{x}y+x\overline{y}$
- (D) $xy+\overline{y}z+\overline{z}$
- (E) $\overline{x}z+xy+\overline{yz}$
Resolução
Primeiramente, vamos construir a tabela da verdade da função $f$ e, em seguida, vamos utilizar a derivação de expressões por soma de produtos (SDP) para obter a expressão booleana de $f$.
| $x$ | $y$ | $z$ | $f(x,y,z)$ | Termos da SDP |
| 0 | 0 | 0 | 0 | - |
| 0 | 0 | 1 | 0 | - |
| 0 | 1 | 0 | 1 | $\overline{x}.y.\overline{z}$ |
| 0 | 1 | 1 | 1 | $\overline{x}.y.z$ |
| 1 | 0 | 0 | 1 | $x.\overline{y}.\overline{z}$ |
| 1 | 0 | 1 | 1 | $x.\overline{y}.z$ |
| 1 | 1 | 0 | 0 | - |
| 1 | 1 | 1 | 0 | - |
Agora, vamos somar os termos da última coluna e simplificar a expressão
$$ \begin{align*}f(x,y,z)&=\overline{x}.y.\overline{z}+\overline{x}.y.z+x.\overline{y}.\overline{z}+x.\overline{y}.z\\&=\overline{x}.y.(\overline{z}+z)+x.\overline{y}.(\overline{z}+z)\\&=\overline{x}.y+x.\overline{y}\\\end{align*}$$
Portanto, alternativa correta é a C.
Questões 25 e 26
Assunto: linguagens formais e autômatos (índice).
As soluções dessas questões podem ser obtidas na postagem Questões do POSCOMP sobre Linguagens Formais e Autômatos #01.
Questão 27
Assunto: estruturas de dados (índice).
Suponha que T seja uma árvore AVL inicialmente vazia, e considere a inserção dos elementos 10, 20, 30, 5, 15, 2 em T, nesta ordem. Qual das sequências abaixo corresponde a um percurso de T em pré-ordem:
- (A) 10, 5, 2, 20, 15, 30
- (B) 20, 10, 5, 2, 15, 30
- (C) 2, 5, 10, 15, 20, 30
- (D) 30, 20, 15, 10, 5, 2
- (E) 15, 10, 5, 2, 20, 30
Resolução
Primeiramente, vamos montar a árvore AVL fazendo as inserções conforme o enunciado apresenta. A imagem a seguir mostra a construção da árvore passo a passo (clique aqui para baixar a imagem):
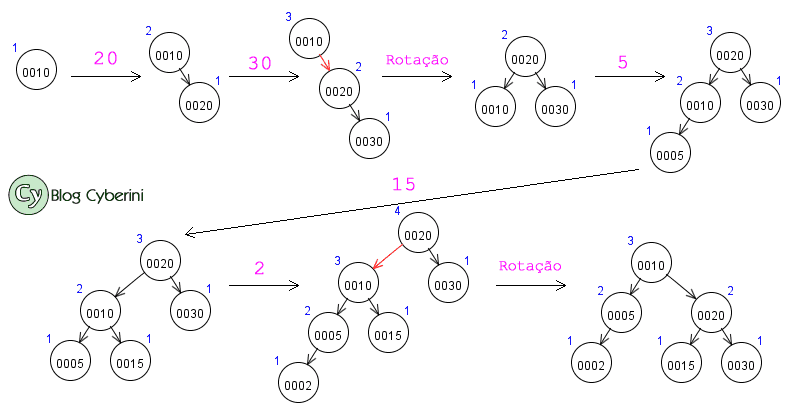
Se preferir, você pode ver a construção passo a passo no seguinte vídeo: Construção da árvore AVL (YouTube). Tanto a imagem como o vídeo foram feitos utilizando um visualizador de estruturas de dados apresentado numa postagem anterior do blog.
Agora, basta realizar o percurso em pré-ordem (raiz-esquerda-direita). A sequência será 10, 5, 2, 20, 15, 30.
Logo, a alternativa correta é a A.
Questão 28
Assunto: estruturas de dados (índice).
Considere uma tabela de espalhamento (tabela hash) com quatro posições numeradas 0, 1, 2 e 3. Se a sequência de quadrados perfeitos 1, 4, 9, ..., $i^2$, ... for armazenada nessa tabela segundo a função $f(x)=x\operatorname{mod} 4$, como se dará a distribuição dos elementos pelas posições da tabela, à medida que o número de entradas cresce?
- (A) Cada posição da tabela receberá aproximadamente o mesmo número de elementos
- (B) Três posições da tabela receberão, cada uma, aproximadamente um terço dos elementos
- (C) Uma única posição da tabela receberá todos os elementos, e as demais posições permanecerão vazias
- (D) Todas as posições da tabela receberão elementos, mas as duas primeiras receberão, cada uma, o dobro das outras
- (E) As duas primeiras posições da tabela receberão, cada uma, aproximadamente a metade dos elementos, e as demais posições permanecerão vazias
Resolução
É conveniente testar a função de hash com alguns valores para analisar o seu comportamento:
- Para o valor 1, temos $f(1) = 1 \operatorname{mod} 4 = 1$;
- Para o valor 4, temos $f(4) = 4 \operatorname{mod} 4 = 0$;
- Para o valor 9, temos $f(9) = 9 \operatorname{mod} 4 = 1$;
- Para o valor 16, temos $f(16) = 16 \operatorname{mod} 4 = 0$;
- Para o valor 25, temos $f(25) = 25 \operatorname{mod} 4 = 1$;
- Para o valor 36, temos $f(36) = 36 \operatorname{mod} 4 = 0$.
Só lembrando que mod é o operador para calcular o resto da divisão. Observe que a posição de inserção será 0 sempre que o número a ser inserido é par. Por outro lado, se o número é ímpar, então a posição de inserção será 1.
Outro ponto importante é que sempre que inserimos um número ímpar, o próximo valor a ser inserido será par e, quando inserimos um par, o próximo valor que vai ser inserido será ímpar, logo cada posição (0 ou 1) receberá aproximadamente o mesmo número de elementos.
Vamos tentar generalizar. O resto da divisão pode ser calculado da seguinte forma
$$x\operatorname{mod} a = x - a\times\left\lfloor\frac{x}{a}\right\rfloor,\,a,x\in\mathbb{Z}$$
No nosso caso, $x = i^2$. Substituindo na fórmula anterior, temos
$$\begin{align*}x\operatorname{mod} 4 &= i^2\operatorname{mod} 4\\&= i^2 - 4\times\left\lfloor\frac{i^2}{4}\right\rfloor\end{align*}$$
Quando $i^2$ é par, temos que $i=2k$, logo
$$\begin{align*}i^2\operatorname{mod} 4&=(2k)^2 - 4\times\left\lfloor\frac{(2k)^2}{4}\right\rfloor\\&=4k^2 - 4\times\left\lfloor\frac{4k^2}{4}\right\rfloor\\&=4k^2 - 4\times\lfloor k^2\rfloor\\&=0\end{align*}$$
Ou seja, se o valor a ser inserido for par, então a posição de inserção sempre será 0.
Se $i^2$ é ímpar, então $i=2k+1$, portanto
$$\begin{align*}i^2\operatorname{mod} 4&=(2k+1)^2 - 4\times\left\lfloor\frac{(2k+1)^2}{4}\right\rfloor\\&=4k^2 + 4k + 1 - 4\times\left\lfloor\frac{4k^2 + 4k + 1}{4}\right\rfloor\\&=4k^2 + 4k + 1 - 4\times\left\lfloor k^2+k+\frac{1}{4} \right\rfloor\\&=4k^2 + 4k + 1 - 4\times\left(k^2+k\right)\\&=1\end{align*}$$
Assim, se o valor a ser inserido for ímpar, então a posição de inserção sempre será 1.
Por fim, a alternativa correta é a E.
Questão 29
Assunto: complexidade de algoritmos (índice).
A questão 29 foi resolvida na postagem Questões do POSCOMP sobre Complexidade de Algoritmos #01.
Nenhum comentário:
Postar um comentário