Merge Sort paralelo em Java

Uma das vantagens do algoritmo de ordenação por intercalação (Merge Sort) é a facilidade de codificá-lo de forma paralela. Isto é, utilizando multithreading.

Em geral, a maioria dos algoritmos de divisão e conquista possui essa característica, que é consequência da independência dos subproblemas gerados na etapa de divisão.

Neste artigo, programaremos o Merge Sort em Java utilizando o modelo Fork-Join.

O modelo Fork/Join em Java

O padrão Fork-Join é um modelo de computação paralela, que consiste em executar paralelamente as tarefas recursivas de um programa num determinado ponto (fork) e, após a conclusão dessas tarefas num outro ponto, o programa passa a ser sequencial, usualmente para processar os resultados obtidos (join) [2].

Ilustração do modelo Fork-Join

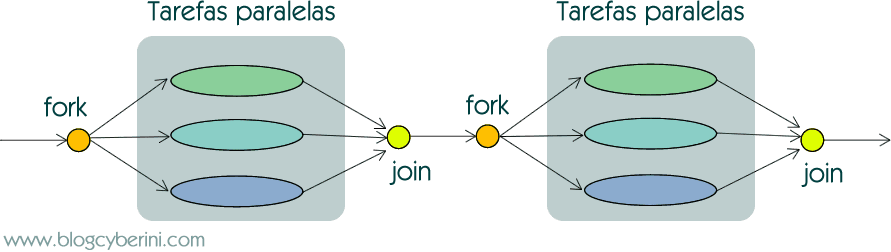
O ponto do programa onde as tarefas são 'paralelizadas' (fork) pode ser uma etapa de divisão de um problema em subproblemas, no qual cada um é independente e, como consequência, a execução paralela é permitida. Aqui, temos uma clara analogia ao paradigma de divisão e conquista.

Na prática, o padrão Fork-Join é perfeito para implementar os algoritmos desse paradigma. Entretanto, nos limitaremos ao Merge Sort.

A linguagem de programação Java, possui classes em sua biblioteca padrão que permitem implementar facilmente programas utilizando o modelo Fork-Join.

As classes básicas são (todas pertencem ao pacote java.util.concurrent) [1]

• RecursiveAction: é utilizada para implementar tarefas que não possuem valor de retorno. É uma subclasse de ForkJoinTask;
• RecursiveTask: é utilizada para tarefas com valor de retorno. Também é uma subclasse de ForkJoinTask;
• ForkJoinPool: é um ExecurtorService para executar ForkJoinTask. Em outras palavras, o ForkJoinPool irá gerenciar e executar as nossas tarefas paralelamente, sendo possível inclusive escolher número de processadores (ou núcleos de processadores) que serão utilizados.

Como o Merge Sort realiza a ordenação no próprio vetor, então não precisamos de valor de retorno, logo nossa opção será a classe RecursiveAction.

Merge Sort com Fork-Join

A seguinte classe em Java implementa uma ação recursiva para ordenar um vetor (int[] array) utilizando o Merge Sort.

//GitHub: HenriqueIni
//https://www.blogcyberini.com/
import java.util.concurrent.RecursiveAction;

public class MergeSortTask extends RecursiveAction {
    private int[] array; //array que será ordenado
    private int inicio; //índice de início
    private int fim; //índice do fim
    
    //ordena o subarray do índice 'inicio' até 'fim'
    public MergeSortTask(int[] array, int inicio, int fim){
        this.array = array;
        this.inicio = inicio;
        this.fim = fim;
    }
    //ordena o array por completo
    public MergeSortTask(int[] array){
        this(array, 0, array.length - 1);
    }
    //executa o MergeSort paralelamente com Fork-Join
    @Override
    protected void compute() {
        if(inicio < fim){
            int meio = (inicio + fim) / 2; //calcula o meio
            //realiza as chamadas recursivas paralelamente (fork)
            invokeAll(new MergeSortTask(array, inicio, meio),
                      new MergeSortTask(array, meio + 1, fim));
            merge(inicio, meio, fim); //intercala os subvetores (join)
        }
    }
    //intercala os subvetores esquerdo e direito
    private void merge(int inicio, int meio, int fim){
        int tamEsq = meio - inicio + 1; //tamanho do subvetor esquerdo
        int tamDir = fim - meio; //tamanho do subvetor direito
        int esq[] = new int[tamEsq]; //subvetor auxiliar esquerdo
        int dir[] = new int[tamDir]; //subvetor auxiliar direito
        int idxEsq = 0; //índice do subvetor auxiliar esquerdo
        int idxDir = 0; //índice do subvetor auxiliar direito
        
        //Copia os elementos do subvetor esquerdo para o vetor auxiliar
        for(int i = 0; i < tamEsq; i++){
            esq[i] = array[inicio + i];
        }
        //Copia os elementos do subvetor direito para o vetor auxiliar
        for(int j = 0; j < tamDir; j++){
            dir[j] = array[meio + 1 + j];
        }
        
        //intercala os subvetores
        for(int k = inicio; k <= fim; k++){
            if(idxEsq < tamEsq){
                if(idxDir < tamDir){
                    if(esq[idxEsq] < dir[idxDir]){
                        array[k] = esq[idxEsq++];
                    }else{
                        array[k] = dir[idxDir++];
                    }
                }else{
                    array[k] = esq[idxEsq++];
                }
            }else{
                array[k] = dir[idxDir++];
            }
        }
    }
}

A classe MergeSortTask é subclasse da classe abstrata RecursiveAction, que possui o método abstrato compute. É nesse método que o algoritmo do Merge Sort é implementado. Os valores de entrada do algoritmo são os atributos de MergeSortTask, passados através dos métodos construtores.

Um objeto da classe MergeSortTask deve ser encarado como se fosse uma chamada recursiva do Merge Sort tradicional. Entretanto, as execuções das chamadas são realizadas pelo método invokeAll. Isto é, criamos os objetos que representam as chamadas recursivas que realizaremos e passamos esses objetos para o método invokeAll executá-los. Essa etapa corresponde ao 'fork'.

Após as tarefas serem concluídas, utilizamos o método merge para fundir os subvetores ordenados (join). O método merge é executado de forma serial (isto é, sem paralelismo), logo nenhuma alteração no merge tradicional é necessária.

Para executar a tarefa, utilizamos um ForkJoinPool. A classe principal a seguir indica como utilizar o ForkJoinPool para executar a nossa tarefa MergeSortTask.

//GitHub: HenriqueIni
//https://www.blogcyberini.com/
import java.util.concurrent.ForkJoinPool;

//códigos de testes do merge sort com Fork Join
public class TestesMergeForkJoin {
    public static void main(String[] args) {        
        ForkJoinPool pool = new ForkJoinPool(); //cria um pool de threads Fork/Join
        int[] A = {5, 2, 7, 6, 2, 1, 0, 3, 9, 4}; //array que será ordenado
        //imprime o vetor desordenado
        System.out.printf("A (desordenado) = [%d, %d, %d, %d, %d, %d, %d, %d, %d, %d]\n",
                A[0], A[1], A[2], A[3], A[4], A[5], A[6], A[7], A[8], A[9]);        
        MergeSortTask mergeTask = new MergeSortTask(A); //tarefa ForkJoin para ordenar o vetor A
        pool.invoke(mergeTask); //executa a tarefa utilizando o pool
        //imprime o vetor ordenado
        System.out.printf("A (ordenado) = [%d, %d, %d, %d, %d, %d, %d, %d, %d, %d]\n",
                A[0], A[1], A[2], A[3], A[4], A[5], A[6], A[7], A[8], A[9]);
        
        /*
         * Você também pode utilizar o método 'Arrays.parallelSort(vetor)'
         * para ordenar vetores utilizando múltiplas threads
         */
    }    
}

Download do código

Os códigos em Java anteriores também podem ser obtidos nos links abaixo

• Merge Sort paralelo em Java no Google Drive
• Merge Sort paralelo em Java no GitHub

Considerações finais

A implementação paralela apresentada neste artigo é apenas uma das possibilidades para o Merge Sort. Acredito que seja a mais fácil, pois não precisamos nos preocupar com a sincronização das threads – o próprio Java se encarrega de tudo.

A biblioteca padrão da linguagem Java também possui o método Arrays.parallelSort(vetor), que realiza a ordenação de um array qualquer utilizando multithreading. Se você quiser apenas um método para ordenar vetores que aproveite todos os processadores do seu computador, então opte por essa última opção, pois, em geral, métodos nativos são mais eficientes.

Referências

• [1] Oracle. The Java™ Tutorials - Fork/Join. Acesso em 23 de julho de 2018.
• [2] Wikipedia - Fork-join model. Acesso em 23 de julho de 2018.