O Merge Sort (ordenação por intercalação/fusão) é um algoritmo de ordenação recursivo cujo mérito pela criação é atribuído ao físico e matemático John von Neumann.
A complexidade no tempo desse algoritmo de divisão e conquista é $O(n\log n)$, sendo mais eficiente do que os algoritmos Bubble Sort, Selection Sort e Insertion Sort, que já foram analisados em artigos anteriores do blog.
Neste artigo, será realizada uma análise do Merge Sort. Como é de costume, também disponibilizarei o algoritmo codificado em Java, C e em JavaScript.
Índice
Como funciona o Merge Sort?
A ideia do Merge Sort é dividir o vetor em dois subvetores, cada um com metade dos elementos do vetor original. Esse procedimento é então reaplicado aos dois subvetores recursivamente.
Quando os subvetores têm apenas um elemento (caso base), a recursão para. Então, os subvetores ordenados são fundidos (ou intercalados) num único vetor ordenado.
Como exemplo, ordenaremos o vetor [5, 2, 7, 6, 2, 1, 0, 3, 9, 4]. Inicialmente, dividimos o vetor em dois subvetores, cada um com metade dos elementos do vetor original.
Reaplicamos o método aos dois subvetores
De novo,
Mais uma vez, pois ainda não alcançamos o caso base em alguns subvetores
Finalmente, fazemos a fusão dos subvetores
O diagrama a seguir ilustra todas as etapas
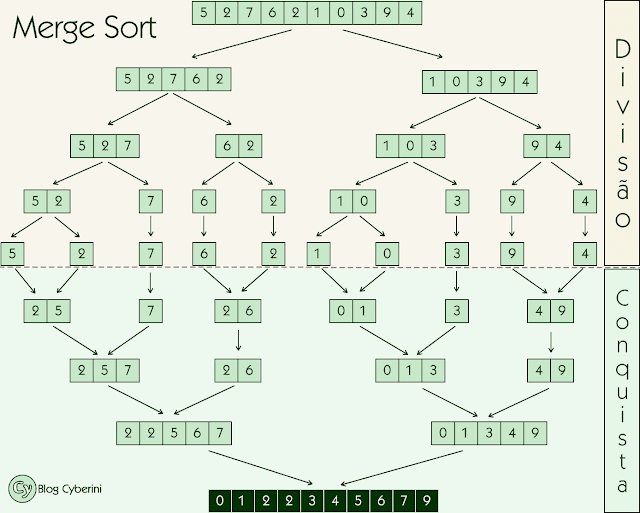
No exemplo, várias etapas foram realizadas simultaneamente para não estender o artigo. Entretanto, na realidade, o Merge Sort ordena os subvetores um por vez.
Podemos realizar algumas etapas paralelamente se tivermos à nossa disposição um processador com mais de um núcleo. Para isso, o Merge Sort precisa ser codificado para que possa utilizar múltiplas threads.
Merge Sort em pseudocódigo
Como vimos, o Merge Sort possui duas etapas
- divisão do vetor em subvetores até atingirmos o caso base;
- fusão dos subvetores (
merge).
A primeira etapa consiste no seguinte algoritmo
01. mergesort(A[0...n - 1], inicio, fim) 02. | se(inicio < fim) 03. | | meio ← (inicio + fim) / 2 //calcula o meio 04. | | mergesort(A, inicio, meio) //ordena o subvetor esquerdo 05. | | mergesort(A, meio + 1, fim) //ordena o subvetor direito 06. | | merge(A, inicio, meio, fim) //funde os subvetores esquerdo e direito 07. | fim_se 08. fim_mergesort
A etapa de fusão é [1]
01. merge(A[0...n - 1], inicio, meio, fim) 02. | tamEsq ← meio - inicio + 1 //tamanho do subvetor esquerdo 03. | tamDir ← fim - meio //tamanho do subvetor direito 04. | inicializar vetor Esq[0...tamEsq - 1] 05. | inicializar vetor Dir[0...tamDir - 1] 06. | para i ← 0 até tamEsq - 1 07. | | Esq[i] ← A[inicio + i] //elementos do subvetor esquerdo 08. | fim_para 09. | para j ← 0 até tamDir - 1 10. | | Dir[j] ← A[meio + 1 + j] //elementos do subvetor direito 11. | fim_para 12. | idxEsq ← 0 //índice do subvetor auxiliar esquerdo 13. | idxDir ← 0 //índice do subvetor auxiliar direito 14. | para k ← inicio até fim 15. | | se(idxEsq < tamEsq) 16. | | | se(idxDir < tamDir) 17. | | | | se(Esq[idxEsq] < Dir[idxDir]) 18. | | | | | A[k] ← Esq[idxEsq] 19. | | | | | idxEsq ← idxEsq + 1 20. | | | | senão 21. | | | | | A[k] ← Dir[idxDir] 22. | | | | | idxDir ← idxDir + 1 23. | | | | fim_se 24. | | | senão 25. | | | | A[k] ← Esq[idxEsq] 26. | | | | idxEsq ← idxEsq + 1 27. | | | fim_se 28. | | senão 29. | | | A[k] ← Dir[idxDir] 30. | | | idxDir ← idxDir + 1 31. | | fim_se 32. | fim_para 33. fim_merge
Observe que o método merge utiliza dois vetores auxiliares. A utilização desses vetores faz com o Merge Sort tenha complexidade $O(n)$ no espaço.
Por causa da cópia de elementos entre os vetores auxiliares e o vetor A, a complexidade no tempo do método merge é $\Theta(n)$ ou $O(n)$.
Alternativamente, podemos utilizar um único vetor auxiliar na ordenação, porém a complexidade no tempo e no espaço será a mesma.
Complexidade assintótica
A equação de recorrência do Merge Sort é [1]
$$T(n)=2T(n/2)+\Theta(n)$$
O termo $2T(n/2)$ é o tempo para ordenar dois vetores de tamanho $n/2$, já o termo $\Theta(n)$ é o tempo para fundir/intercalar esses vetores, isto é, é o tempo do método merge.
A equação de recorrência anterior já foi resolvida algumas vezes em postagens anteriores do blog, porém resolveremos de novo.
Podemos utilizar o método de Akra-Bazzi ou o método mestre na resolução. Optaremos pelo segundo.
De acordo com o teorema mestre, temos
$$a=2,\quad b=2,\quad f(n)=\Theta(n)$$
Além disso,
$$\log_b a=\log_2 2=1$$
Como $f(n)=\Theta\left(n^{\log_b a}\right)=\Theta(n)$, então a equação de recorrência satisfaz o segundo caso do teorema mestre, portanto
$$T(n)=\Theta\left(n^{\log_b a}\log n\right)=\Theta(n\log n)$$
Ou, equivalentemente, $T(n)=O(n\log n)$. Essa complexidade é a mesma no melhor caso, no caso médio e no pior caso.
Se quiser saber como resolver a equação de recorrência do Merge Sort através do método de Akra-Bazzi, acesse postagem: O Método de Akra-Bazzi na Resolução de Equações de Recorrência.
Códigos
Os códigos em Java, C e em JavaScript do Merge Sort podem ser obtidos nos links a seguir
Referências
- [1] CORMEN, T. H. et al. Algoritmos: teoria e prática. 3 ed. Rio de Janeiro: Elsevier, 2012.
Nenhum comentário:
Postar um comentário