Nesta postagem, você encontrará a resolução de 16 questões de matemática do POSCOMP 2002, além do gabarito das outras quatro questões que não foram resolvidas.
Índice
- Questão 01
- Questão 02
- Questão 03
- Questão 04
- Questão 05
- Questão 07
- Questão 08
- Questão 09
- Questão 10
- Questão 12
- Questão 13
- Questão 14
- Questão 15
- Questão 17
- Questão 18
- Questão 19
- Outras questões
- Referências
Para mais questões resolvidas, acesse a página POSCOMP.
Questão 01
Pode-se afirmar que gráfico da função $y=2+\cfrac{1}{x-1}$ é o gráfico da função $y=\cfrac{1}{x}$
- (A) transladado uma unidade para a direita e duas unidades para cima;
- (B) transladado uma unidade para a direita e duas unidades para baixo;
- (C) transladado uma unidade para a esquerda e duas unidades para cima;
- (D) transladado uma unidade para a esquerda e duas unidades para baixo;
- (E) nenhuma das anteriores.
Resolução
É possível transformar a função $f(x)=\cfrac{1}{x}$ em $g(x)=2+\cfrac{1}{x-1}$ somando 2 à $f(x)$ e subtraindo 1 de $x$.
Ao somar o valor 2, a função é deslocada duas unidades para cima.
Subtrair 1 de $x$ é o mesmo que realizar a transformação $x=x'-1$. Isolando a coordenada $x'$, temos
$$x'=x+1$$
Isso significa que $f(x)$ foi deslocada para direita
Logo, a opção correta é a A.
Questão 02
A derivada da função $f(x)=x^x$ é igual a
- (A) $xx^{x-1}$
- (B) $x^x$
- (C) $x^x\ln x$
- (D) $x^x(\ln x + 1)$
- (E) $x^x(\ln x + x)$
Resolução
Em síntese, a questão deseja $\cfrac{df}{dx}$. Inicialmente, vamos calcular o logaritmo natural de $f(x)$
$$\begin{align*}\ln f(x) = \ln x^x\\\ln f(x) = x\ln x\end{align*}$$
Agora, vamos derivar ambos os membros da expressão anterior
$$\begin{align*}\frac{d}{dx}\ln f(x)=\frac{d}{dx}(x\ln x)\\\frac{1}{f}\frac{df}{dx} = \left(x\frac{1}{x}+\ln x\right)\\\frac{df}{dx}=\left(1+\ln x\right)f\end{align*}$$
Como $f(x)=x^x$, então vamos substituir o $f$ no lado direito da equação
$$\frac{df}{dx} = x^x\left(1+\ln x\right)$$
Portanto, a alternativa correta é a D.
Questão 03
Seja $n$ um número inteiro positivo. Considere a função $f$ definida recursivamente por
$$f(n)=\begin{cases}0&\mbox{se } n=1\\f\left(\left\lfloor\frac{n}{2}\right\rfloor\right)+1&\mbox{se }n > 1\end{cases}$$
onde $\left\lfloor\cfrac{n}{2}\right\rfloor$ é o maior inteiro menor ou igual a $k$. O valor de $f(25)$ é igual a
- (A) 5
- (B) 4
- (C) 6
- (D) 3
- (E) 2
Resolução
Indo direto ao ponto, temos
$$\begin{align*}f(25)&= f\left(\left\lfloor\frac{25}{2}\right\rfloor\right)+1\\&=f(12)+1\\&=f\left(\left\lfloor\frac{12}{2}\right\rfloor\right)+1+1\\&=f(6)+1+1\\&=f\left(\left\lfloor\frac{6}{2}\right\rfloor\right)+1+1+1\\&= f(3)+1+1+1\\&=f\left(\left\lfloor\frac{3}{2}\right\rfloor\right)+1+1+1+1\\&= f(1)+1+1+1+1\\&= 0+1+1+1+1\\&=4\end{align*}$$
Ou seja, a resposta certa é B.
Questão 04
Para cada $n\in\mathbb{N}$ seja $D_n=(0,1/n)$, onde $(0,1/n)$ representa o intervalo aberto de extremos $0$ e $1/n$. O conjunto diferença $D_3-D_{20}$ é igual a:
- (A) $D_3$
- (B) $D_{20}$
- (C) $(1/20,1/3)$
- (D) $[1/20,1/3)$
- (E) $D_{20}\cup D_3$
Resolução
Os conjuntos $D_3$ e $D_{20}$ são
$$\begin{align*}D_3=(0,1/3)=(0,0.333\ldots)\\D_{20}=(0,1/20)=(0,0.05)\end{align*}$$
Ou ainda
$$\begin{align*}D_3=\{x\,|\,0<x<1/3\}\\D_{20}=\{x\,|\,0<x<1/20\}\end{align*}$$
A diferença $D_3-D_{20}$ contém todos os elementos de $D_3$ que não são elementos de $D_{20}$. Ou seja, os elementos do conjunto $D_3-D_{20}$ são todos os elementos $x\in D_3$ tais que $x\geq 1/20$, logo
$$\begin{align*}D_3-D_{20}&=\{x\,|\,1/20\leq x < 1/3\}\\&=[1/20, 1/3)\end{align*}$$
Portanto, a alternativa D é a correta.
Questão 05
Todos os convidados presentes num jantar tomam chá ou café. Treze convidados bebem café, dez bebem chá e 4 bebem chá e café. Quantas pessoas tem nesse jantar?
- (A) 19
- (B) 27
- (C) 23
- (D) 15
- (E) 10
Resolução
O problema é bem simples. Primeiro, vamos calcular quantas pessoas bebem apenas café e quantas bebem apenas chá
- Pessoas que bebem apenas café: $13 - 4 = 9$;
- Pessoas que bebem apenas chá: $10 - 4 = 6$.
Fizemos isso porque dentro do conjunto de pessoas que bebem café existem também pessoas que bebem chá. Por outro lado, dentro do conjunto de pessoas que bebem chá também existem pessoas que bebem café. Observe o diagrama a seguir
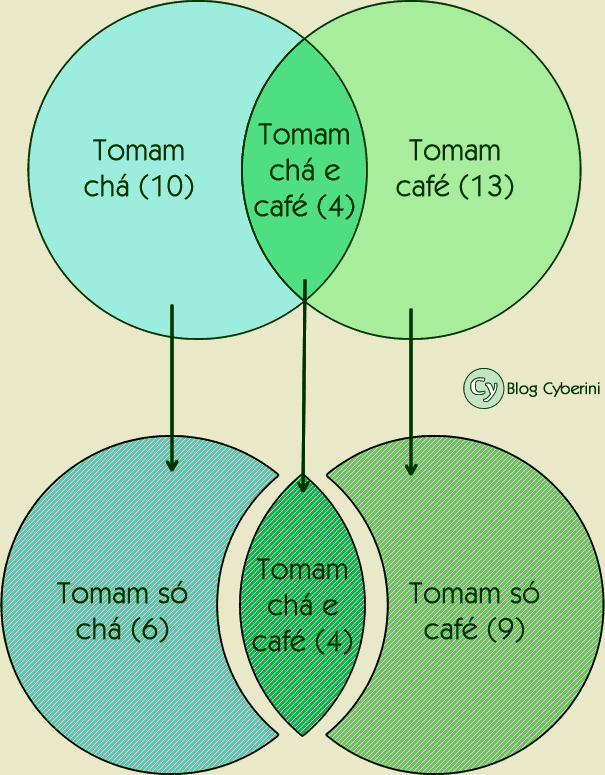
Agora, basta somar o número de pessoas que só tomam chá, o número de pessoas que só tomam café e o número de pessoas que tomam chá e café:
$$9+6+4=19$$
Portanto, a alternativa correta é a A.
Questão 07
Seja $f:\mathbb{R}\rightarrow\mathbb{R}$ derivável. Se existem $a,b\in\mathbb{R}$ tal que $f(a)f(b)<0$ e $f'(x)\neq 0$ para todo $x\in (a,b)$, podemos afirmar que no intervalo $(a,b)$ a equação $f(x)=0$ tem
- (A) duas raízes reais
- (B) nenhuma raiz real
- (C) uma única raiz real
- (D) uma raiz imaginária
- (E) somente raízes imaginárias
Resolução
Como $f$ é derivável em $\mathbb{R}$, então também é contínua em $\mathbb{R}$. A expressão$f(a).f(b)<0$ indica que há inversão de sinal em $(a,b)$ e, como $f$ é contínua, deve haver pelo menos uma raiz real no intervalo $(a,b)$.
Por sua vez, a expressão $f'(x)\neq 0$ indica que não há pontos extremos (máximos ou mínimos) em $(a,b)$, portanto apenas uma raiz real é possível em $(a,b)$. Graficamente, teríamos algo do tipo
Portanto, a alternativa correta é a C.
Questão 08
Seja $g:\mathbb{R}\rightarrow\mathbb{R}$ contínua e $f(x)=g(x)-x$. Definimos a sequência $(x_n)$ da seguinte maneira
$$\begin{cases}x_0=1\\x_n=g(x_{n-1})\quad\text{para }n\geq 1\end{cases}$$
Se $\lim_{n\rightarrow\infty}x_n=L$ podemos afirmar que
- (A) $L$ é uma raiz e $f(x)=0$
- (B) $L$ é uma raiz e $g(x)=0$
- (C) $g(L)=1$
- (D) $f(L)=L$
- (E) nenhuma das anteriores
Resolução
Primeiramente, substituímos $x$ por $x_n$ em $f(x)$
$$f(x_n)=g(x_n)-x_n$$
Agora tomamos o limite $n\rightarrow\infty$
$$\begin{align*}\lim_{n\rightarrow\infty} f(x_n)&=\lim_{n\rightarrow\infty}[g(x_n)-x_n]\\f\left(\lim_{n\rightarrow\infty} x_n\right)&=g\left(\lim_{n\rightarrow\infty} x_n\right)-\lim_{n\rightarrow\infty}x_n\end{align*}$$
Como $\lim_{n\rightarrow\infty} x_n=L$, então
$$f(L)= g\left(\lim_{n\rightarrow\infty} x_n\right)-L$$
Numa sequência, $\lim_{n\rightarrow\infty} a_n=\lim_{n\rightarrow\infty} a_{n-1}$. Utilizando essa propriedade na definição da sequência $x_n$, temos
$$\begin{align*}\lim_{n\rightarrow\infty} x_n&=\lim_{n\rightarrow\infty}g(x_{n-1})\\\lim_{n\rightarrow\infty} x_n&= g\left(\lim_{n\rightarrow\infty} x_{n-1}\right)\\\lim_{n\rightarrow\infty} x_n&=g\left(\lim_{n\rightarrow\infty} x_n\right)\\L&= g\left(\lim_{n\rightarrow\infty} x_n\right)\\\end{align*}$$
Substituindo em $f(L)$, temos
$$f(L)=L-L=0$$
Logo, $L$ é uma raiz de $f(x)$ e a alternativa correta é a A.
Questão 09
Assinale a proposição verdadeira
- (A) Se $x$ é um número real tal que $x^2\leq 4$ então $x\leq 2$ e $x\leq -2$
- (B) Se $x$ e $y$ são números reais tais que $x<y$ então $x^2<y^2$
- (C) Se $x+y$ é um número racional então $x$ e $y$ são números racionais
- (D) Se $x<-4$ ou $x>1$ então $\cfrac{2x+3}{x-1}>1$
- (E) nenhum das anteriores
Resolução
A alternativa A está incorreta, pois o conjunto solução de $x^2\leq 4$ é $[-2,2]$ ou $-2\leq x \leq 2$.
A alternativa B está incorreta. Se tomarmos $x=-3$ e $y = 1$, por exemplo, teremos $-3<1$, que é verdade, mas isso implicaria em $9<1$, que é falso.
A alternativa C está incorreta. Se tomarmos $x=1+\sqrt{2}$ e $x=1-\sqrt{2}$, então $x+y=2$ é um número racional, entretanto $x$ e $y$ são irracionais.
A alternativa D está correta. Para demonstrar isso, vamos resolver a inequação da alternativa
Quando $x-1>0$, então
$$\begin{align*}\frac{2x+3}{x-1}>1\\2x+3>x-1\\x>-4\end{align*}$$
Como $x-1>0$ é equivalente a $x>1$, então a solução será $x>1$ e $x>-4$, ou simplesmente $x>1$.
Quando $x-1<0$, então
$$\begin{align*}\frac{2x+3}{x-1}>1\\2x+3<x-1\\x<-4\end{align*}$$
Como $x-1<0$ é equivalente a $x<1$, então a solução será $x<1$ e $x<-4$, ou simplesmente $x<-4$. A inversão do sentido da desigualdade ocorreu porque multiplicamos ambos os membros da inequação por $x-1$, que é negativo.
Portanto, a solução é $x>1$ ou $x<-4$. Sempre que $x$ satisfizer essas condições, a inequação será verdadeira. Com isso, concluímos a demonstração de que a alternativa D é a correta.
Questão 10
Assinale o argumento válido, onde S1, S2 indicam premissas e S a conclusão:
- (A)
S1: Se o cavalo estiver cansado então ele perderá a corridaS2: O cavalo estava descansadoS: O cavalo ganhou a corrida
- (B)
S1: Se o cavalo estiver cansado então ele perderá a corridaS2: O cavalo ganhou a corridaS: O cavalo estava descansado
- (C)
S1: Se o cavalo estiver cansado então ele perderá a corridaS2: O cavalo perdeu a corridaS: O cavalo estava cansado
- (D)
S1: Se o cavalo estiver cansado então ele perderá a corridaS2: O cavalo estava descansadoS: O cavalo perdeu a corrida
- (E) nenhuma das anteriores
Resolução
Observe que a premissa S1 é a mesma em A, B, C e D. Vamos considerar as seguintes proposições
p: cavalo cansadoq: ganhar a corrida
Com isso, S1 será p→¬q. Para não estender o texto, analisaremos apenas a alternativa B, que é a correta.
Em B, a premissa S2 é q (ganhar a corrida). A conclusão S é ¬p (cavalo descansado). Logo, temos que mostrar que a expressão S1∧S2→S é sempre verdadeira.
S1 ∧ S2 → S = (p → ¬q) ∧ q → ¬p S1 ∧ S2 → S = (¬p ∨ ¬q) ∧ q → ¬p S1 ∧ S2 → S = (¬p ∧ q) ∨ (¬q ∧ q) → ¬p S1 ∧ S2 → S = (¬p ∧ q) ∨ FALSO → ¬p S1 ∧ S2 → S = (¬p ∧ q) → ¬p S1 ∧ S2 → S = ¬(¬p ∧ q) ∨ ¬p S1 ∧ S2 → S = p ∨ ¬q ∨ ¬p S1 ∧ S2 → S = p ∨ ¬p ∨ ¬q S1 ∧ S2 → S = VERDADEIRO ∨ ¬q S1 ∧ S2 → S = VERDADEIRO
Também podemos utilizar uma tabela da verdade:
p |
q |
S1 (p → ¬q) |
S2 (q) |
S1 ∧ S2 |
S (¬p) |
S1 ∧ S2 → S |
|---|---|---|---|---|---|---|
| F | F | V | F | F | V | V |
| F | V | V | V | V | V | V |
| V | F | V | F | F | F | V |
| V | V | F | V | F | F | V |
Com isso, concluímos a demonstração de que B é a alternativa correta.
Questão 12
Dado um vetor $u\in R^2$, $u=(-3,4)$, vamos denotar por $v$ o vetor de $R^2$ que tem tamanho 1 e é ortogonal à $u$. Então $v$ por ser dado por
- (A) $(−4/5, 3/5)$
- (B) $(3/5, 4/5)$
- (C) $(−4/5,−3/5)$
- (D) $(−4/5, 1/5)$
- (E) $(−4/5, 2/5)$
Resolução
Suponhamos que $v=(x,y)$. Para que $v$ seja ortogonal a $u$, o produto escalar entre os dois vetores deve ser zero
$$\begin{align*}&v\cdot u=0\\&(x,y)\cdot (-3,4)=0\\&-3x+4y=0\end{align*}$$
A equação anterior possui um conjunto infinito de soluções. Felizmente, a questão quer que $v$ tenha tamanho 1.
$$\begin{align*}\sqrt{x^2+y^2}&=1\\x^2+y^2&=1\end{align*}$$
Isolando $x$ na equação $-3x+4y=0$, temos
$$x=\frac{4}{3}y$$
Consequentemente,
$$\begin{align*}\left(\frac{4}{3}y\right)^2+y^2&=1\\\frac{16}{9}y^2+\frac{9}{9}y^2&=1\\\frac{25}{9}y^2&=1\\y^2&=\frac{9}{25}\\y&=\pm\frac{3}{5}\end{align*}$$
Já a componente $x$ é dada por
$$x=\pm\frac{4}{3}.\frac{3}{5}=\pm\frac{4}{5}$$
Ou seja, existem dois vetores que satisfazem as condições da questão
$$v_1=\left(\frac{4}{5},\frac{3}{5}\right);\quad v_2=\left(-\frac{4}{5},-\frac{3}{5}\right)$$
Portanto, a alternativa correta é a C.
Questão 13
Se $O=(0,0,0)$; $A=(2,4,1)$; $B=(3,1,1)$ e $C=(1,3,5)$ então o volume do sólido acima é
- (A) 30
- (B) 35
- (C) 35/2
- (D) 44
- (E) 21
Resolução
O sólido da questão é um paralelepípedo. Podemos calcular o seu volume calculando o módulo do determinante da matriz composta pelos vetores A, B e C, que definem o sólido [1]. Ou seja,
$$V= \left|\det\begin{bmatrix}2 & 4& 1\\3 & 1 & 1\\1 & 3 & 5\end{bmatrix}\right|$$
O determinante pode ser calculado pela regra de Sarrus (ou pelo teorema de Laplace)
$$V=|-1-6-60+10+4+9|=|-44|=44$$
Portanto, a alternativa correta é a D.
Questão 14
A velocidade de um ponto em movimento é dada pela equação
$$v(t)=te^{-0.01t}$$
O espaço percorrido desde o instante que o ponto começou a se mover até a sua parada total é
- (A) $10^4$ m
- (B) $10^3e^{-0.01}$ m
- (C) $10^2e^{-1}$ m
- (D) $(e^{-100}-1)$ m
- (E) $10^2$ m
Resolução
Analisando a função $v(t)$, vemos que ela se anula quando $t=0$ e quando $t\rightarrow\infty$, que são, respectivamente, o instante de início e o de parada do movimento.
Portanto, o espaço percorrido será
$$S=\int_0^{\infty}v(t)dt=\int_0^{\infty}te^{-0.01t}dt$$
Vamos calcular a integral por partes
$$\begin{align*}&u=t\\&du=dt\\&dv=e^{-0.01t}dt\\&v=\int e^{-0.01t}dt=-100e^{-0.01t}\end{align*}$$
$$\begin{align*}&\int t e^{-0.01t}dt=\\&=-100te^{-0.01t}-\int -100e^{-0.01t}dt\\&=-100te^{-0.01t}-\int -100e^{-0.01t}dt\\&=-100te^{-0.01t}+100\int e^{-0.01t}dt\\&=-100te^{-0.01t}+100\times (-100)e^{-0.01t}\\&=-e^{-0.01t}(100t+10000)\end{align*}$$
Finalmente, calculamos $S$
$$\begin{align*}S&=\left.-e^{-0.01t}(100t+10000)\right|_{0}^{\infty}\\&=\lim_{t\rightarrow\infty}\left[-e^{-0.01t}(100t+10000)\right]- \left[-e^{-0.01\times 0}(100\times 0+10000)\right]\\&=0+e^{0}\times 10000\\&=10^4\text{m}\end{align*}$$
Logo, a alternativa A é a correta.
Questão 15
Se $\lim_{n\rightarrow\infty}\frac{1}{n^2}+\frac{2}{n^2}+\ldots+\frac{n-1}{n^2}=L$ então
- (A) $L=1$
- (B) $L=0$
- (C) $L=1/2$
- (D) $L=\infty$
- (E) $L=2$
Resolução
Inicialmente, vamos simplificar a expressão entre parênteses
$$\begin{align*}&\frac{1}{n^2}+\frac{2}{n^2}+\ldots+\frac{n-1}{n^2}=\\&= \frac{1}{n^2}(1+2+\ldots+n-1)\\&= \frac{1}{n^2}\sum_{i=1}^{n-1} 1\\&=\frac{1}{n^2}\frac{n(n-1)}{2}\\&=\frac{n^2-n}{2n^2}\\&=\frac{n^2}{2n^2}-\frac{n}{2n^2}\\&=\frac{1}{2}-\frac{1}{2n}\end{align*}$$
Tomando o limite $n\rightarrow\infty$, temos
$$\lim_{n\rightarrow\infty}\left(\frac{1}{2}-\frac{1}{2n}\right)=\frac{1}{2}=L$$
Portanto, a alternativa C é a correta.
Questão 17
A média aritmética de uma lista de 50 números é 50. Se dois desses números, 51 e 97, forem suprimidos dessa lista a média dos restantes será
- (A) 50
- (B) 49
- (C) 51
- (D) 47
- (E) 40
Resolução
A média aritmética, $m$, de uma lista de números é igual à soma dos números, $S$, dividida pela quantidade de números, $n$
$$m=\frac{S}{n}$$
Para a lista do enunciado, temos
$$50=\frac{S}{50}\Rightarrow S = 2500$$
Se removermos os 51 e o 97 da lista (dois números), a média será
$$\frac{2500-51-97}{50-2}=\frac{2352}{48}=49$$
Portanto, a alternativa correta é a B.
Questão 18
O determinante da matriz dada abaixo é
$$\begin{bmatrix}2 & 7 & 9 & -1 & 1\\2 & 8 & 3 & 1 & 0\\-1 & 0 & 4 & 3 & 0\\2 & 0 & 0 & -1 & 0\\3 & 0 & 0 & 0 & 0\end{bmatrix}$$
- (A) 96
- (B) -96
- (C) 86
- (D) -86
- (E) 46
Resolução
Se trocarmos a primeira coluna e a última de posição, o determinante da matriz terá o sinal invertido, porém a matriz se tornará triangular
$$\begin{bmatrix}1 & 7 & 9 & -1 & 2\\0 & 8 & 3 & 1 & 2\\0 & 0 & 4 & 3 & -1\\0 & 0 & 0 & -1 & 2\\0 & 0 & 0 & 0 & 3\end{bmatrix}$$
O determinante de uma matriz triangular é igual ao produto dos elementos da diagonal principal. Com isso, o determinante será
$$D=-[1\times 8\times 4\times (-1)\times 3]=96$$
O sinal negativo é necessário porque o sinal do determinante foi invertido quando fizemos a troca de colunas.
Portanto, a alternativa correta é a A.
Questão 19
Numa prova de múltipla escolha com 10 questões e 4 alternativas qual a chance (probabilidade) de um aluno apenas "chutando as respostas" conseguir "gabaritar" a prova (acertar todas as questões).
- (A) $1/10^4$
- (B) $1/4^{20}$
- (C) $1/2^{20}$
- (D) $1/10^8$
- (E) $1/4^{15}$
Resolução
A probabilidade de acertar uma questão é de $1/4$. A probabilidade de acertar 10 questões será
$$\begin{align*}P&=\left(\frac{1}{4}\right)^{10}\\&=\left(\frac{1}{2^2}\right)^{10}\\&= \frac{1}{2^{2\times 10}}\\&=\frac{1}{2^{20}}\end{align*}$$
Na última etapa, foi utilizada a propriedade da potência de potência.
A alternativa correta é a C.
Outras questões
Deixo aqui o gabarito das questões que não foram resolvidas nesta postagem
- 06 - E
- 11 - E
- 16 - C
- 20 - C
Referências
- [1] DANTE, L. R. Matemática, Volume único. 1ª edição. São Paulo: Ática, 2005.
Nenhum comentário:
Postar um comentário