Quicksort paralelo em Java utilizando o modelo Fork-Join

Uma das vantagens dos algoritmos de divisão e conquista, como o Quicksort, é a simplicidade de implementá-los de forma paralela.

Nesta postagem, veremos como implementar quatro versões do Quicksort (Cormen, Hoare, mediana de três e aleatorizado) na linguagem de programação Java utilizando o padrão Fork-Join, que é um padrão de computação paralela.

Quicksort paralelo em Java com Fork-Join

Sugiro que o leitor leia o artigo Quicksort (análise e implementações) para melhor compreensão, caso não conheça o Quicksort.

Se quiser informações sobre outros algoritmos de ordenação, acesse o tópico Algoritmos de Ordenação.

Quicksort com Fork-Join

Nesta seção, darei uma breve explicação do modelo Fork-Join, pois ele já foi abordado no artigo Merge Sort paralelo em Java, onde apresento a implementação do Merge sort utilizando esse modelo.

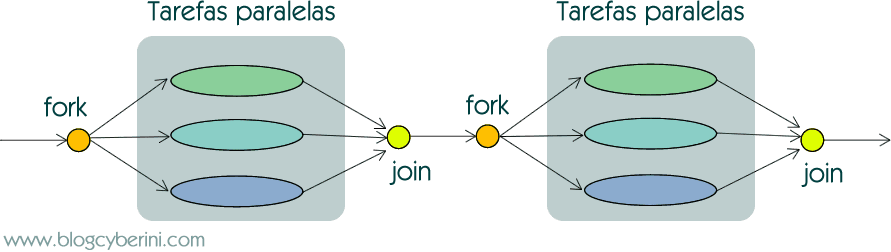
A ideia do modelo (ou padrão) Fork-Join é realizar a bifurcação (fork) do fluxo de execução do programa em diversas tarefas, que são executadas paralelamente. Então, em um ponto posterior, essas tarefas se "encontram" (join) e o fluxo de execução do programa passa a ser sequencial [2].

Normalmente, o ponto de encontro (ou junção) é onde os resultados obtidos por cada tarefa são processados.

Em Java, o modelo pode ser facilmente implementado utilizando as classes RecursiveAction, RecursiveTask e ForkJoinPool [1].

No caso do Quicksort, sua implementação paralela pode ser feita utilizando a classe abstrata RecursiveAction, que corresponde a uma tarefa sem valor de retorno.

Cada chamada recursiva corresponderá a um objeto da classe RecursiveAction (especificamente, de uma subclasse que implementaremos).

Ir para o índice

Códigos

Os códigos em Java podem ser obtidos nos links abaixo. Se preferir, copie os códigos incorporados no artigo.

Ir para o índice

Quicksort de Hoare

O Quicksort de Hoare escolhe como pivô o elemento que está no início do vetor.

//GitHub: HenriqueIni
//https://www.blogcyberini.com/
import java.util.concurrent.RecursiveAction;

public class QuicksortForkJoinHoare extends RecursiveAction {
    private int[] array; //array que será ordenado
    private int inicio; //índice de início
    private int fim; //íncide do fim

    //ordena o subarray do índice 'inicio' até 'fim'
    public QuicksortForkJoinHoare(int[] array, int inicio, int fim){
        this.array = array;
        this.inicio = inicio;
        this.fim = fim;
    }
    //ordena o array por completo
    public QuicksortForkJoinHoare(int[] array){
        this(array, 0, array.length - 1);
    }
    //executa o Quicksort paralelamente com Fork-Join
    @Override
    protected void compute() {
        if(inicio < fim){
            int q = partition(array, inicio, fim); //obtém o pivô (join)
            //realiza as chamadas recursivas paralelamente (fork)
            invokeAll(new QuicksortForkJoinHoare(array, inicio, q - 1),
                      new QuicksortForkJoinHoare(array, q + 1, fim));
        }
    }
    //Método de partição
    private static int partition(int[] A, int inicio, int fim){
        //o pivo é o elemento inicial
        int pivo = A[inicio];
        //índice i irá percorrer o array da esquerda para a direita
        int i = inicio + 1;
        //índice j irá percorrer o array da direita para a esquerda
        int j = fim;

        //O loop irá parar quando os índices se ultrapassarem
        while(i <= j){
            /*
             * Este laço irá parar quando encontrar algum elemento
             * à esquerda que é maior que o pivô, pois ele deveria estar na
             * partição direita
             */
            while(i <= j && A[i] <= pivo){
                i = i + 1;
            }
            /*
             * Esse laço irá parar quando encontrar algum elemento
             * à direira que é menor ou igual ao pivô, pois ele deveria estar na
             * partição esquerda
             */
            while(i <= j && A[j] > pivo){
                j = j - 1;
            }

            //se os índices não ultrapassarem, troca-os de posição
            if(i < j){
                swap(A, i, j);
            }
        }
        //coloca o pivô na posição de ordenação
        swap(A, inicio, j);
        return j; //retorna a posição do pivô
    }

    //método auxiliar para realizar as trocas de elementos
    private static void swap(int[] A, int i, int j){
        int temp = A[i];
        A[i] = A[j];
        A[j] = temp;
    }
}

Ir para o índice

Quicksort de Cormen

O Quicksort de Cormen [3] escolhe como pivô o elemento que está no final do vetor.

//GitHub: HenriqueIni
//https://www.blogcyberini.com/
import java.util.concurrent.RecursiveAction;

public class QuicksortForkJoinCormen extends RecursiveAction {
    private int[] array; //array que será ordenado
    private int inicio; //índice de início
    private int fim; //íncide do fim

    //ordena o subarray do índice 'inicio' até 'fim'
    public QuicksortForkJoinCormen(int[] array, int inicio, int fim){
        this.array = array;
        this.inicio = inicio;
        this.fim = fim;
    }
    //ordena o array por completo
    public QuicksortForkJoinCormen(int[] array){
        this(array, 0, array.length - 1);
    }
    //executa o Quicksort paralelamente com Fork-Join
    @Override
    protected void compute() {
        if(inicio < fim){
            int q = partition(array, inicio, fim); //obtém o pivô (join)
            //realiza as chamadas recursivas paralelamente (fork)
            invokeAll(new QuicksortForkJoinCormen(array, inicio, q - 1),
                      new QuicksortForkJoinCormen(array, q + 1, fim));
        }
    }
    //Método de partição
    private static int partition(int[] A, int inicio, int fim){
        //o pivo é o elemento final
        int pivo = A[fim];
        int i = inicio - 1;
        /*
         * Este laço irá varrer os vetores da esquerda para direira
         * procurando os elementos que são menores ou iguais ao pivô.
         * Esses elementos são colocados na partição esquerda.
         */
        for(int j = inicio; j <= fim - 1; j++){
            if(A[j] <= pivo){
                i = i + 1;
                swap(A, i, j);
            }
        }
        //coloca o pivô na posição de ordenação
        swap(A, i + 1, fim);
        return i + 1; //retorna a posição do pivô
    }

    //método auxiliar para realizar as trocas de elementos
    private static void swap(int[] A, int i, int j){
        int temp = A[i];
        A[i] = A[j];
        A[j] = temp;
    }
}

Ir para o índice

Quicksort de mediana de três

O Quicksort mediana de três escolhe como pivô a mediana entre os elementos no início, meio e fim do vetor.

//GitHub: HenriqueIni
//https://www.blogcyberini.com/
import java.util.concurrent.RecursiveAction;

public class QuicksortForkJoinMedianThree extends RecursiveAction {
    private int[] array; //array que será ordenado
    private int inicio; //índice de início
    private int fim; //íncide do fim

    //ordena o subarray do índice 'inicio' até 'fim'
    public QuicksortForkJoinMedianThree(int[] array, int inicio, int fim){
        this.array = array;
        this.inicio = inicio;
        this.fim = fim;
    }
    //ordena o array por completo
    public QuicksortForkJoinMedianThree(int[] array){
        this(array, 0, array.length - 1);
    }
    //executa o Quicksort paralelamente com Fork-Join
    @Override
    protected void compute() {
        if(inicio < fim){
            int q = partition(array, inicio, fim); //obtém o pivô (join)
            //realiza as chamadas recursivas paralelamente (fork)
            invokeAll(new QuicksortForkJoinMedianThree(array, inicio, q - 1),
                      new QuicksortForkJoinMedianThree(array, q + 1, fim));
        }
    }
    //Método de partição
    private static int partition(int[] A, int inicio, int fim){
        //procura a mediana entre inicio, meio e fim
        int meio = (inicio + fim)/2;
        int a = A[inicio];
        int b = A[meio];
        int c = A[fim];
        int medianaIndice; //índice da mediana
        //A sequência de if...else a seguir verifica qual é a mediana
        if(a < b){
            if(b < c){
                //a < b && b < c
                medianaIndice = meio;
            }else{
                if(a < c){
                    //a < c && c <= b
                    medianaIndice = fim;
                }else{
                    //c <= a && a < b
                    medianaIndice = inicio;
                }
            }
        }else{
            if(c < b){
                //c < b && b <= a
                medianaIndice = meio;
            }else{
                if(c < a){
                    //b <= c && c < a
                    medianaIndice = fim;
                }else{
                    //b <= a && a <= c
                    medianaIndice = inicio;
                }
            }
        }
        //coloca o elemento da mediana no fim para poder usar o Quicksort de Cormen
        swap(A, medianaIndice, fim);

        //*******************ALGORITMO DE PARTIÇÃO DE CORMEN*********************
        //o pivo é o elemento final
        int pivo = A[fim];
        int i = inicio - 1;
        /*
         * Este laço irá varrer os vetores da esquerda para direira
         * procurando os elementos que são menores ou iguais ao pivô.
         * Esses elementos são colocados na partição esquerda.
         */
        for(int j = inicio; j <= fim - 1; j++){
            if(A[j] <= pivo){
                i = i + 1;
                swap(A, i, j);
            }
        }
        //coloca o pivô na posição de ordenação
        swap(A, i + 1, fim);
        return i + 1; //retorna a posição do pivô
    }

    //método auxiliar para realizar as trocas de elementos
    private static void swap(int[] A, int i, int j){
        int temp = A[i];
        A[i] = A[j];
        A[j] = temp;
    }
}

Ir para o índice

Quicksort de com pivô aleatório

Como o nome sugere, o Quicksort com pivô aleatório escolhe como pivô um elemento aleatório do vetor.

//GitHub: HenriqueIni
//https://www.blogcyberini.com/
import java.util.Random;
import java.util.concurrent.RecursiveAction;

public class QuicksortForkJoinRandomized  extends RecursiveAction {
    private int[] array; //array que será ordenado
    private int inicio; //índice de início
    private int fim; //íncide do fim
    private static final Random RANDOM_NUMBER_GEN = new Random(); //gera números aleatórios

    //ordena o subarray do índice 'inicio' até 'fim'
    public QuicksortForkJoinRandomized(int[] array, int inicio, int fim){
        this.array = array;
        this.inicio = inicio;
        this.fim = fim;
    }
    //ordena o array por completo
    public QuicksortForkJoinRandomized(int[] array){
        this(array, 0, array.length - 1);
    }
    //executa o Quicksort paralelamente com Fork-Join
    @Override
    protected void compute() {
        if(inicio < fim){
            int q = partition(array, inicio, fim); //obtém o pivô (join)
            //realiza as chamadas recursivas paralelamente (fork)
            invokeAll(new QuicksortForkJoinRandomized(array, inicio, q - 1),
                      new QuicksortForkJoinRandomized(array, q + 1, fim));
        }
    }
    //Método de partição
    private static int partition(int[] A, int inicio, int fim){
        //sorteia um índice aleatório entre inicio e fim
        int randomIndex = RANDOM_NUMBER_GEN.nextInt(fim - inicio + 1) + inicio;
        //coloca o pivô aleatório no fim para aplicar a partição de Cormen
        swap(A, randomIndex, fim);

        //*******************ALGORITMO DE PARTIÇÃO DE CORMEN*********************
        //o pivo é o elemento final
        int pivo = A[fim];
        int i = inicio - 1;
        /*
         * Este laço irá varrer os vetores da esquerda para direira
         * procurando os elementos que são menores ou iguais ao pivô.
         * Esses elementos são colocados na partição esquerda.
         */
        for(int j = inicio; j <= fim - 1; j++){
            if(A[j] <= pivo){
                i = i + 1;
                swap(A, i, j);
            }
        }
        //coloca o pivô na posição de ordenação
        swap(A, i + 1, fim);
        return i + 1; //retorna a posição do pivô
    }

    //método auxiliar para realizar as trocas de elementos
    private static void swap(int[] A, int i, int j){
        int temp = A[i];
        A[i] = A[j];
        A[j] = temp;
    }
}

Ir para o índice

Código de testes

O código abaixo mostra como utilizar o ForkJoinPool e as classes anteriores. O ForkJoinPool é um pool de threads para tarefas Fork-Join, que gerencia a execução das mesmas. É subclasse de AbstractExecutorService.

//GitHub: HenriqueIni
//https://www.blogcyberini.com/
import java.util.concurrent.ForkJoinPool;

public class TestesQuicksortForkJoin {
    public static void main(String[] args) {
        //cria um pool de threads Fork/Join
        ForkJoinPool pool = new ForkJoinPool();
        
        //array que será ordenado
        int[] A = {5, 2, 7, 6, 2, 1, 0, 3, 9, 4};
        
        //imprime o vetor desordenado
        System.out.println("A (desordenado) = " + arrayToString(A));
        
        //***TESTA O QUICKSORT DE CORMEN***
        //tarefa ForkJoin para ordenar o vetor A
        QuicksortForkJoinCormen quicksortTaskCormen = new QuicksortForkJoinCormen(A);
        //executa a tarefa utilizando o pool
        pool.invoke(quicksortTaskCormen);
        System.out.println("A (ordenado com Quicksort de Cormen) = " + arrayToString(A));
        
        //***TESTA O QUICKSORT DE HOARE***
        //gera um novo array
        A = new int[]{5, 2, 7, 6, 2, 1, 0, 3, 9, 4};
        //tarefa ForkJoin para ordenar o vetor A
        QuicksortForkJoinHoare quicksortTaskHoare = new QuicksortForkJoinHoare(A);
        //executa a tarefa utilizando o pool
        pool.invoke(quicksortTaskHoare);
        System.out.println("A (ordenado com Quicksort de Hoare) = " + arrayToString(A));
        
        //***TESTA O QUICKSORT MEDIANA DE 3***
        //gera um novo array
        A = new int[]{5, 2, 7, 6, 2, 1, 0, 3, 9, 4};
        //tarefa ForkJoin para ordenar o vetor A
        QuicksortForkJoinMedianThree quicksortTaskMedianThree = new QuicksortForkJoinMedianThree(A);
        //executa a tarefa utilizando o pool
        pool.invoke(quicksortTaskMedianThree);
        System.out.println("A (ordenado com Quicksort Mediana de 3) = " + arrayToString(A));
        
        //***TESTA O QUICKSORT COM PIVÔ ALEATÓRIO***
        //gera um novo array
        A = new int[]{5, 2, 7, 6, 2, 1, 0, 3, 9, 4};
        //tarefa ForkJoin para ordenar o vetor A
        QuicksortForkJoinRandomized quicksortTaskRandom = new QuicksortForkJoinRandomized(A);
        //executa a tarefa utilizando o pool
        pool.invoke(quicksortTaskRandom);
        System.out.println("A (ordenado com Quicksort com pivô aleatório) = " + arrayToString(A));
    }
    
    //Método auxiliar para imprimir os arrays
    private static String arrayToString(int[] array){
        String aux = "[" + array[0];
        for(int i = 1; i < array.length; i++){
            aux += ", " + array[i];
        }
        return aux + "]";
    }
    
}

Ir para o índice

Considerações finais

A principal vantagem de utilizar o padrão Fork-Join com Java é que a implementação é mais prática, uma vez que não precisamos nos preocupar com a sincronização de threads.

Os algoritmos apresentados neste artigo não devem ser utilizados em situações práticas, pois a implementação paralela do Quicksort não elimina os casos patológicos do algoritmo.

Caso você esteja precisando de um método para ordenar vetores utilizando o paralelismo, recomendo a utilização o método Arrays.parallelSort(vetor), que pertence à biblioteca padrão do Java.

Ir para o índice

Referências

[1] Oracle. The Java™ Tutorials - Fork/Join. Acesso em 05 de setembro de 2018.
[2] Wikipédia - Modelo Fork-Join. Acesso em 05 de setembro de 2018.
[3] CORMEN, T. H. et al. Algoritmos: teoria e prática. 3 ed. Rio de Janeiro: Elsevier, 2012.

Quicksort paralelo em Java utilizando o modelo Fork-Join

Índice

Quicksort com Fork-Join

Códigos

Quicksort de Hoare

Quicksort de Cormen

Quicksort de mediana de três

Quicksort de com pivô aleatório

Código de testes

Considerações finais

Referências

Siga o blog

Nenhum comentário:

Postar um comentário

Potenciação de Matrizes

Questões Resolvidas do ENADE 2017 de Ciência da Computação

Como obter o ID de um canal do YouTube?

Teorema Mestre e Exemplos Resolvidos

Algoritmo da Equação do Quarto Grau

Bubble Sort