POSCOMP 2019: Questão 01 Resolvida (Álgebra Linear)

Questão

Seja uma matriz quadrada de terceira ordem $A=\begin{bmatrix}2 & 3 & 5\\7 & 11 & 13\\17 & 19 & 23\end{bmatrix}$, calcule o determinante:

• (A) Det A = -78
• (B) Det A = -84
• (C) Det A = 84
• (D) Det A = 78
• (E) Det A = -87

Resolução

Para encontrar o determinante da matriz em questão, vamos utilizar a Regra de Sarrus. Para tanto, repetimos as duas primeiras colunas no final da matriz, formando a matriz estendida.

Agora, multiplicamos os elementos das diagonais, trocando os sinais dos elementos à esquerda.

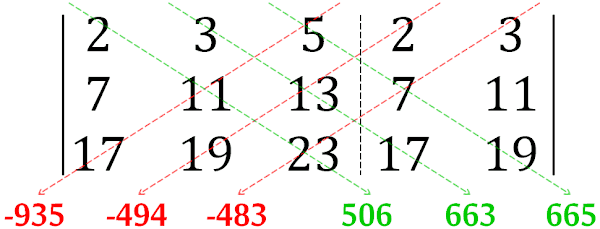
Por fim, o determinante será a soma dos produtos calculados anteriormente:

$$\begin{align*}\det A &= (-935)+(-494)+(-483)+506+663+665\\&= -935-494-483+506+663+665\\&= -78\\\end{align*}$$

Portanto, a alternativa A é a correta.

Mais questões

Se você deseja mais questões resolvidas do POSCOMP 2019, acesse a tag Questões do POSCOMP 2019.

Agora, se você procura questões, gabaritos e caderno de questões de outras edições, então acesse a página POSCOMP.

Resolverei as questões conforme o tempo permitir e de acordo com os meus conhecimentos. Como eu não sei resolver todas as questões, recomendo que você consulte também o gabarito oficial do exame.