POSCOMP 2019: Questão 02 Resolvida (Álgebra Linear)

Questão

Seja $E=\mathbb{R}^3$. Os vetores $\{(1, 2, 3), (2, 5, 8), (1, 3, 7)\}$ são independentes?

• (A) Não.
• (B) Sim.
• (C) Não pode ser calculado.
• (D) Sim, se fosse no espaço de $\mathbb{R}^2$
• (E) Seriam independentes se o 1º vetor fosse $(1,5,7)$.

Resolução

Para resolver esta questão, utilizaremos a seguinte notação para representar os vetores

$$\begin{align*}\vec{v}&=(1,2,3)\\\vec{u}&=(2,5,8)\\\vec{w}&=(1,3,7)\end{align*}$$

A seguir, apresentarei duas formas de resolver este problema.

Primeira forma de resolução

O primeiro método de resolução consiste em utilizar o conceito de independência linear de vetores.

Esse conceito diz que os vetores de conjunto de vetores em $\mathbb{R}^n$ é linearmente independente se nenhum dos vetores for uma combinação linear dos demais vetores [1].

Matematicamente, isso significa que, dado um conjunto de vetores $\{\vec{v}_1, \vec{v}_2,\ldots, \vec{v}_n\}$, onde $\vec{v}_i\in\mathbb{R}^n$, a expressão a seguir só será válida se as constantes $a_i$ forem iguais a zero [1]

$$a_1\vec{v}_1+ a_2\vec{v}_2+\ldots+ a_n\vec{v}_n=\vec{0}.$$

Aqui, $\vec{0}$ é o vetor nulo. No nosso problema, toda essa teoria pode ser traduzida na seguinte expressão

$$\begin{align*}&a\vec{v}+b\vec{u}+c\vec{w}=\vec{0}\\&a(1,2,3)+b(2,5,8)+c(1,3,7)=(0,0,0).\end{align*}$$

Os vetores $\vec{v}$, $\vec{u}$ e $\vec{w}$, serão independentes se expressão acima for satisfeita apenas quando as constantes $a$, $b$ e $c$ forem iguais a zero.

Desenvolvendo a expressão, obtemos

$$\begin{align*}(a,2a,3a)+(2b,5b,8b)+(c,3c,7c)&=(0,0,0)\\(a+2b+c,2a+5b+3c,3a+8b+7c) &=(0,0,0).\end{align*}$$

Igualando as componentes dos vetores, obteremos o seguinte sistema linear homogênio 3×3

$$\begin{cases}a+2b+c=0\\2a+5b+3c=0\\3a+8b+7c=0\end{cases}$$

Em forma matricial, temos

$$\begin{bmatrix}1 & 2 & 1\\2 & 5 & 3\\3 & 8 & 7\end{bmatrix}\begin{bmatrix}a\\ b\\ c\end{bmatrix}=\begin{bmatrix}0\\0\\ 0\end{bmatrix}.$$

Num sistema linear homogênio, se o determinante da matriz dos coeficientes for zero, então ele é possível e indeterminado, tendo infinitas soluções. Por outro lado, se o determinante não for zero, então ele admitirá apenas a solução trivial, isto é, $(0,0,0,\ldots,0)$ [2].

Em outras palavras, se o determinante da matriz de coeficientes for zero, então os vetores serão linearmente dependentes. Se for diferente de zero, então os vetores serão linearmente independentes, já que a expressão $a\vec{v}+b\vec{u}+c\vec{w}=\vec{0}$ só será válida se as constantes $a$, $b$ e $c$ forem iguais a zero.

Finalmente, calculando o determinante via Regra de Sarrus, temos

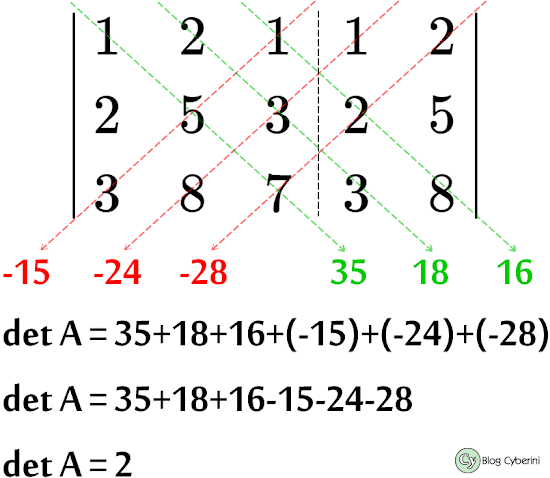
Como o determinante é diferente de zero, então os vetores são linearmente independentes, logo a resposta B é a correta.

Segunda forma de resolução

Se você sobreviveu a toda essa explicação teórica, temos boas notícias: existe um método mais rápido para resolver o problema! Para isso, basta calcular o determinante da matriz formada pelos vetores [2].

Distribuímos os vetores $\vec{v}$, $\vec{u}$ e $\vec{w}$ nas linhas de uma matriz:

$$\begin{bmatrix}\vec{v}\\\vec{u}\\\vec{w}\end{bmatrix}=\begin{bmatrix}1 & 2 & 3\\2 & 5 & 8\\1 & 3 & 7\\\end{bmatrix}$$

Agora, basta calcular o determinante:

Como o determinante é diferente de zero, então os vetores são linearmente independentes.

Ou seja, mais uma vez confirmamos que a alternativa correta é a B.

Mais questões

Se você deseja mais questões resolvidas do POSCOMP 2019, acesse a tag Questões do POSCOMP 2019.

Agora, se você procura questões, gabaritos e caderno de questões de outras edições, então acesse a página POSCOMP.

Resolverei as questões conforme o tempo permitir e de acordo com os meus conhecimentos. Como eu não sei resolver todas as questões, recomendo que você consulte também o gabarito oficial do exame.

Referências

• [1] REMAT (UFRGS). Dependência e independência linear. Disponível em <https://www.ufrgs.br/reamat/AlgebraLinear/livro/s3-dependx00eancia_e_independx00eancia_linear.html>. Acesso em 03 de novembro de 2019.
• [2] DANTE, L. R. Matemática, volume único. 1 ed. São Paulo: Ática, 2005.