POSCOMP 2019: Questão 04 Resolvida (Geometria Analítica)

Questão

Encontre as coordenadas do centro (C) da circunferência de equação $t: x^2+ y^2-3x + 5y-14 = 0$.

• (A) $C\left(\cfrac{1}{2},\cfrac{1}{2}\right)$
• (B) $C\left(\cfrac{-1}{2},\cfrac{3}{2}\right)$
• (C) $C\left(\cfrac{3}{2},\cfrac{1}{2}\right)$
• (D) $C\left(\cfrac{5}{2},\cfrac{5}{2}\right)$
• (E) $C\left(\cfrac{3}{2},\cfrac{-5}{2}\right)$

Resolução

A equação de uma circunferência com centro $C(a,b)$ e raio $r$ é dada por [1]

$$(x-a)^2+(y-b)^2=r^2.$$

Ao expandir a equação anterior, obtemos a equação geral da circunferência

$$x^2+y^2-2ax-2by+(a^2+b^2-r^2)=0$$

Igualando os coeficientes da equação geral da circunferência com os coeficientes da equação $t$, temos

$$\begin{align*}-2a=-3&\Leftrightarrow a=\frac{3}{2}\\-2b=5&\Leftrightarrow a=-\frac{5}{2}\end{align*}$$

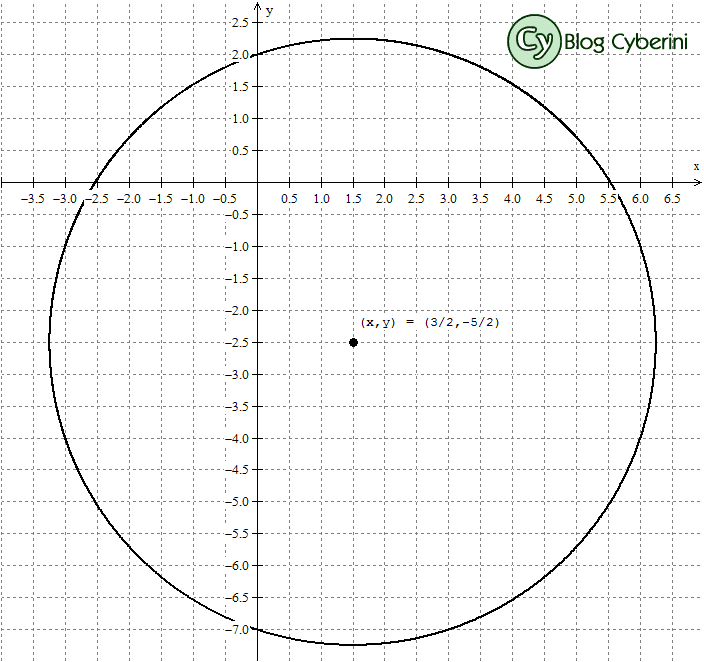
Logo, o centro da circunferência $t$ é $C\left(\cfrac{3}{2},-\cfrac{5}{2}\right)$. Ou seja, a alternativa E é a correta.

Gráfico com a circunferência da questão e o centro dela destacado.

Mais questões

Se você deseja mais questões resolvidas do POSCOMP 2019, acesse a tag Questões do POSCOMP 2019.

Agora, se você procura questões, gabaritos e caderno de questões de outras edições, então acesse a página POSCOMP.

Resolverei as questões conforme o tempo permitir e de acordo com os meus conhecimentos. Como eu não sei resolver todas as questões, recomendo que você consulte também o gabarito oficial do exame.

Referências

• [1] DANTE, L. R. Matemática, volume único. 1 ed. São Paulo: Ática, 2005.