POSCOMP 2019: Questão 09 Resolvida (Circuitos Digitais)

Questão

Simplifique, com a ajuda dos Mapas de Karnaugh, a função cuja expressão em termos canônicos é: $f(x,y,z)=\Sigma\,m(2,3,4,5,6,7)$

• (A) $f(x,y,z)=x+y$
• (B) $f(x,y,z)=x+y+z$
• (C) $f(x,y,z)=\overline{x}+y$
• (D) $f(x,y,z)=xy+y$
• (E) $f(x,y,z)=x+y+\overline{z}$

Resolução

Primeiramente, elaboramos o mapa de Karnaugh de três variáveis.

Os números em verde enumeram as oito situações possíveis para uma função de três variáveis ($2^3=8$).

Conforme a função, as posições 2, 3, 4, 5, 6 e 7 do mapa devem ser preenchidas com $1$. As demais posições serão preenchidas com $0$.

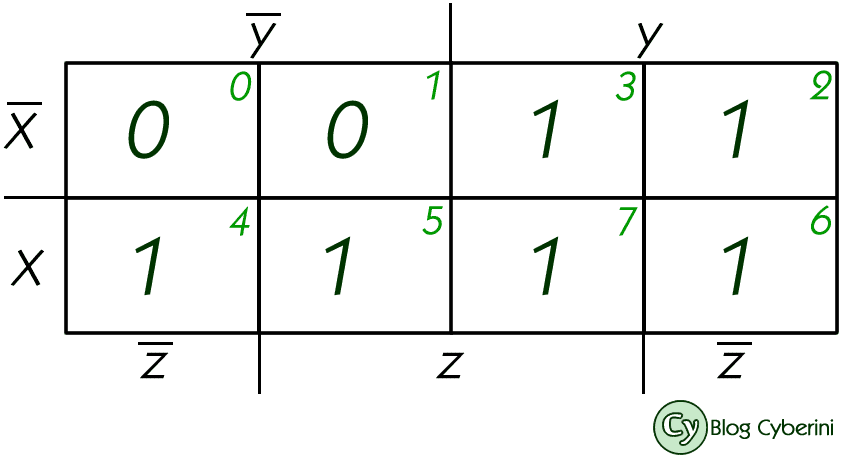
Observe que temos duas regiões que contemplam todos os $1$: a região $x$ e a região $y$.

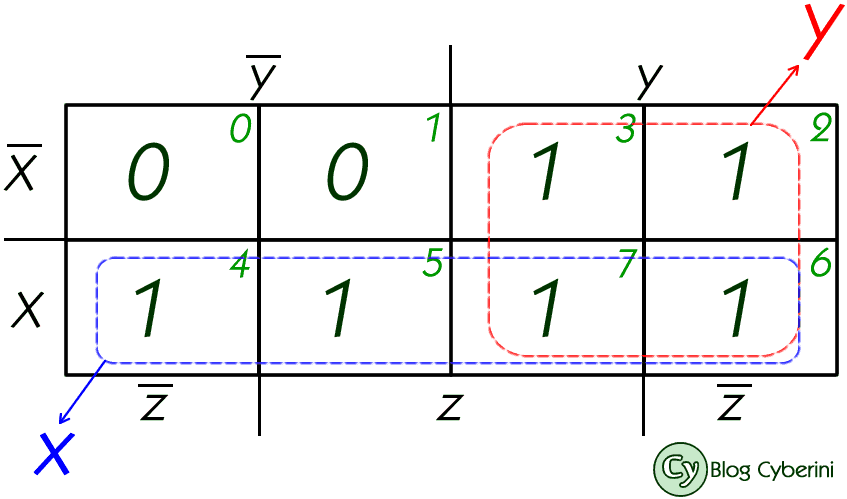
Somando as duas regiões, obtemos

$$f(x,y,z)=x+y.$$

A função anterior é a forma mais simples de $f(x,y,z)$, portanto a alternativa correta é a A.

Mais questões

Se você deseja mais questões resolvidas do POSCOMP 2019, acesse a tag Questões do POSCOMP 2019.

Agora, se você procura questões, gabaritos e caderno de questões de outras edições, então acesse a página POSCOMP.

Resolverei as questões conforme o tempo permitir e de acordo com os meus conhecimentos. Como eu não sei resolver todas as questões, recomendo que você consulte também o gabarito oficial do exame.